Всем добрый день!
Прошу участников форума высказаться по описанной ниже проблеме.
Известно устройство для измерения расстояний под названием курвиметр. Курвиметр состоит из зубчатого ролика и счётчика пройденного количества зубцов. Для измерения длины кривой по ней прокатывают роликом курвиметра [1]. Курвиметр можно использовать двумя способами, - перемещая его вдоль неподвижного измеряемого отрезка, или перемещая измеряемый отрезок по колесу неподвижного курвиметра. Очевидно, что его показания не могут зависеть от того каким из этих двух способов измерять длину отрезка, или, строго говоря, в какой системе отсчета мы производим измерения – в системе отсчета, где неподвижна ось колеса курвиметра, а измеряемый отрезок движется, касаясь колеса курвиметра; или в системе отсчета, где неподвижен измеряемый отрезок, а колесо курвиметра катится по нему. Это не требует доказательства, так как результат (количество зубцов колеса курвиметра) одного и того же физического эксперимента не может зависеть от выбора инерциальной системы отсчета, в которой этот эксперимент рассматривается. Проверим это для случая релятивистских скоростей.
Измерение длины быстро движущегося отрезка Чтобы избежать необходимости учета упругих деформаций в колесе курвиметра при его вращении (парадокс Эренфеста [4 с.38]), немного модифицируем колесо. Пусть колесо представляет собой набор из

тонких жестких одинаковых стержней, лежащих в одной плоскости, и одним концом жестко закреплённых в точке

, являющейся центром колеса (фрагмент такого колеса изображен на рис. 1). Стержни распределены равномерно по кругу. То есть, колесо представляет собой набор спиц, делящих круг на равные сегменты, но без обода (внешние концы спиц никуда не прикреплены).
По определению, собственной длиной отрезка называется его длина в той системе отсчета, в которой он покоится [3 с.27]. Пусть собственная длина

измеряемого отрезка

равна собственной длине окружности, на которой лежат незакрепленные, внешние концы спиц колеса. Тогда, приняв

сколь угодно большим, собственная длина

отрезка

, соединяющего внешние концы двух соседних спиц, равна:


Рис. 1. Колесо курвиметра катится по неподвижному отрезку прямой.
Найдем, что покажет такой курвиметр в системе отсчета, где отрезок

неподвижен, а колесо катится по нему без проскальзывания с некоторой скоростью

(рис. 1). На любом участке движения колеса длина отрезка

, который соединяет внешние концы соседних спиц, соприкасающихся с измеряемым отрезком

, равна его собственной длине

, т.к. отрезок

неподвижен. Следовательно, чтобы пройти от начала до конца отрезка

, последовательно отмеряя спицами интервалы

, – колесу курвиметра потребуется

своих сегментов. Таким образом, в системе отсчета, где отрезок

неподвижен, наш курвиметр зафиксирует длину отрезка

, равную

сегментам колеса.
Перейдем в систему отсчета, связанную с центром вращения колеса курвиметра. В этой системе отсчета колесо равномерно вращается вокруг неподвижной точки

, а отрезок

движется со скоростью

(рис. 2).

Рис. 2. Колесо курвиметра касается движущегося отрезка прямой.
В этой системе отсчета длина спиц колеса не подвержена Лоренцеву сокращению [2 с.74; 3 с.27; 4 с.38], поэтому длина окружности, на которой лежат незакрепленные, внешние концы спиц колеса, равна

. В силу симметрии колеса, длина

отрезка

, соединяющего внешние концы двух соседних спиц, равна собственной длине отрезка

:

Отрезок

в этой системе отсчета в результате Лоренцева сокращения имеет меньшую длину [2 с.18, 74; 3 с.27]:

где

> 1 – Лоренц-фактор.
Чтобы пройти от начала до конца отрезка

, последовательно отмеряя спицами интервалы

, – колесу курвиметра потребуется

своих сегментов. Подставив в это уравнение выражения для

и

, получим:

Таким образом, в системе отсчета, где неподвижен центр колеса, наш курвиметр зафиксирует длину отрезка

, равную
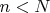
, т.е. отличную от зафиксированной в системе отсчета, где неподвижен отрезок

, что является логическим противоречием.
Список литературы1. Большая советская энциклопедия. – М.: Советская энциклопедия. 1969 –1978
2. Эйнштейн А. Собрание научных трудов. В 4 т. Т.I. Работы по теории относительности 1905-1920; под редакцией И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: НАУКА, 1965
3. Ландау Л.Д., Лившиц Е.М. Теоретическая физика: Учеб. пособие. В 10 т. Т.II. Теория поля. – 7-е изд., испр. – М.: НАУКА, 1988
4. Эренфест П. ОТНОСИТЕЛЬНОСТЬ КВАНТЫ СТАТИСТИКА. Сборник статей. – М.: НАУКА, 1972



