Доброго времени суток.
Вневписанная окружность равнобедренного треугольника касается его боковой стороны.
а) Докажите, что радиус этой окружности равен высоте треугольника, опущенной на основание.
б) Известно, что радиус этой окружности в 4 раза больше радиуса вписанной окружности треугольника. В каком отношении точка касания вписанной окружности с боковой стороной треугольника делит эту сторону?
Рисунок:

Рисунок не очевиден, просто так красиво получилось

. Забыл ввести обозначения высот. Ну, пусть

-- высота треугольника, а
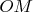
-- радиус вневписанной окружности.
а) Думаю, надо сводить все к банальному четырехугольнику. То есть доказать прямоугольность в углах

и

. Пока идей нет.
б) Зная соотношение, допустим

. Поскольку мы уже как бы потенциально доказали равенство высоты и радиуса вневписанной окружности, то

. Дальше, либо что-то надо достраивать, либо рассматривать прямоугольную (?) трапецию. Очевидно же надо как-нибудь выйти на какие-нибудь подобия. Или нет. Есть идеи?



