BBCode теги включены, все ошибки исправлены в теме post906980.html#p906980 . Прошу вернуть тему на форум.
Не все:
a меньше b, x, y, z
\sum\
x, a, b
n=3, n=5
Не оформлено.
Это некорректное соотношение:
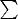
- это оператор суммирования последовательности, сумма может быть определенной или неопределенной, оператор не может быть взять от ничего. Переформулируйте высказывание корректно.
Далее, псевдодоказательство для

пишите перед псевдодоказательством для всех

.
Из приведенных расчетов следует, что многочлены (2), (3), а, следовательно, и (1) не являются уравнениями (не имеют решений), что доказывает справедливость теоремы Ферма.
Рассуждение имеет вид неполной индукции:

, т.е. заведомо неверно.



