В работе буду использовать вероятностные оценки.
Знаю некоторое предубеждение против вероятностных оценок. Постараюсь его рассеять в этой работе.
Известна одна из форм асимптотического закона простых чисел:

, (1)
где

- количество простых чисел, не превосходящих натуральное число

.
Еще в работах Чебышева делается попытка оценки величины:

(2).
В теореме 324 (Бухштаб) показана справедливость оценки:

. (3)
Чебышев показал, что

. В дальнейших работах были получены значения

более близкие к 1.
Из оценки (3) следует:

. (4)
Однако оценки (4) являются весьма грубыми вида:

. (5)
Асимптотический закон о простых числах дает более точную оценку для величины

с использованием интегрального логарифма:

. (6)
При предположении справедливости гипотезы Римана точность формулы (6) дается выражением:

. (7)
Существует также формула Лежандра:

(8).
Но формула (8) менее точна, чем формула (6).
Возникает вопрос - можно ли получить лучшую вероятностную оценку для точности формулы

(9)?
Рассмотрим следующую вероятностную модель.
Пусть имеется

- шаров, неразличимых на ощупь. Пронумеруем их последовательными натуральными числами от 1 до

и положим в урну.
Выберем из урны на удачу один шар и если его номер принадлежит заранее выбранной целочисленной, положительной, инъективной последовательности, то будем считать это событие "успехом", а если номер шара не принадлежит выбранной последовательности, то будем считать это событие "неудачей". Предположим, что вероятность успешного события равна

. Соответственно вероятность неудачного события будет

.
Введем случайную величину

индикатор успешности события. Значение

, если был успех,

, если - неудача.
Вернем шар в урну, перемешаем шары в урне и выберем на удачу 2-ой шар из урны и если его номер принадлежит выбранной последовательности, то присвоим случайной величине

. Если не принадлежит, то -

. Затем вернем 2-ой шар в урну и.т.д. Проделаем это

раз. Таким образом, мы получим последовательность случайных величин - индикаторов успешности событий:

.
Математическое ожидание случайной величины

равно:

(10).
Дисперсия случайной величины

равна:

. (11)
Рассмотрим случайную величину, равную сумме величин:

(12).
Обратим внимание, что

является количеством членов выбранной целочисленной, положительной, инъективной последовательности, не превышающих значение

.
Определим характеристики

.
Ввиду линейности математических ожиданий, математическое ожидание

на основании (10) и (12) равно:

. (13)
Ввиду независимости случайных величин

дисперсия

на основании (11) и (12) равна:

. (14)
Итак мы имеем взаимно независимые, одинаково распределенные случайные величины

, для которых ограничены дисперсии. Поэтому для случайной величины их суммы

справедлива центральная предельная теорема:

, (15)
где

- вероятность выполнения события, указанного в скобках, а

- функция стандарного нормального распределения в точке С.
Подставим полученные характеристики случайной величины

- (13), (14) в выражение (15):

. (16)
Формулу (16) можно получить другим путем, если учесть, что случайная величина

имеет биномиальное распределение, используя частный случай центральной предельной теоремы - теорему Муавра-Лапласа.
Теорему Муавра-Лапласа можно сформулировать следующим образом. Для биномиального закона распределения существует предельное распределение при количестве испытаний, стремящемся к бесконечности

и это предельное распределение является нормальным.
Формулу (16) можно сравнить с неравенством Чебышева.
Запишем формулу Чебышева для данного случая:

. (17)
Например, если

, то по формуле (16) получим, что вероятность указанного события равна

, а по формуле (17) вероятность данного события равна

.
Таким образом, формула (16) значительно точнее формулы (17). Это связано с тем, что формула (17) не учитывает закон распределения случайной величины.
При

вероятность, определяемая по формуле (16) равна

, т.е событие

при

является практически достоверным событием.
На основании свойств нормального распределения, с ростом

, величина

быстро стремится к 1.
Таким образом, можно выбрать такое значение

, чтобы вероятность события:

(18) была сколь угодно близка к 1.
Это является преимуществом вероятностных оценок, так как дает выбор конкретного значения

. Например, оценки (18), по сравнению с формулой (7), по которой оценку точности вообще нельзя проводить.
Последовательность простых чисел является целочисленной, положительной, строго возрастающей, т.е. инъективной.
Ранее было доказано, что для такой последовательности

ее плотность на интервале натурального ряда [
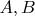
), определяемая по формуле:

(19) (где

- количество членов последовательности

на интервале [
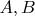
) ), является конечной вероятностной мерой.
Также было показано, что для последовательности простых чисел, на основании асимптотического закона простых чисел и формулы (19), вероятность, что наудачу выбранное натуральное число из интервала

, является простым, равна:

. (20)
Формулу (16), для последовательности простых чисел, на основании (20), можно записать в виде:


, (21) где

- количество простых чисел, не превосходящих натуральное число

.
На основании (21) при

можно выбрать такое значение

, чтобы вероятность события:

(22) была сколь угодно близка к 1.
Проанализируем формулу (22). Она дает оценку сверху для отклонения количества простых чисел, не превышающих

-

, от значения

, т.е. оценку точности для формулы (9).
Саму оценку можно преобразовать к виду:

. (23)
Для (23) выполняется неравенство:

. (24)
Таким образом, на основании (24), при

можно выбрать такое значение

, чтобы вероятность события:

(25) была сколь угодно близка к 1.
На основании наилучшего приближения для

, установленного еще Чебышевым, получим, что наилучшим приближением, для

является функция:

. (26)
Подставляя (26) в (25) получаем:

. (27)
Известно, что эквивалентной формулировкой гипотезы Римана является соотношение:

(28) при

.
Ранее я уже говорил о преимуществе вероятностных оценок, что можно выбрать конкретное значение

в зависимости от требуемой вероятности события.
Если сравнивать оценки (27) и (28), то при

(с вероятностью

) оценки (27) и (28) примерно совпадают. Оценка (27) примерно на 30% выше. Однако, если подставить (26) в (23), то разница сокращается до 20%.
При

(с вероятностью

) оценка (27) лучше оценки (28), начиная с

.
Отсюда вытекает, что при

справедливо следующее соотношение для оценок точности, доказанных вероятностными методами, и оценкой точности, полученной при предположении верности гипотезы Римана:

. (29)
Постоянные

в нижней оценке и

в верхней оценке в формуле (29) можно уточнить с учетом дробных значений.
Буду благодарен за замечания и предложения участников форума.



