Всем привет!
Всем известно, что сфера

(обозначим как просто

) гомотопически эквивалентна плоскости

(обозначим как

). Для того чтобы это показать нужно построить два отображения

такие, что

гомотопны тождественным отображениям. Если я не ошибаюсь, достаточно в качестве

взять тождественное отображение (полагая, что

), а в качестве

взять отображение переводящее точку

в точку

(сфера

единичного радиуса)

. При этом

, и полагая

(тогда

) получим, что

и таким образом эквивалентность

показана.
В ходе решения этой задачи у меня возник другой вопрос. Можно ли каким-нибудь образом задать биекцию

?
У меня здесь в принципе две идеи. Обе проблемные.
1. Отображение
![$f: (1,\varphi) \longmapsto (-\ln \left[1-\frac{\varphi }{2 \pi }\right],\lambda \varphi)$ $f: (1,\varphi) \longmapsto (-\ln \left[1-\frac{\varphi }{2 \pi }\right],\lambda \varphi)$](https://dxdy-01.korotkov.co.uk/f/4/e/2/4e261cc1f2adcaa73d83377d2e3e1d9782.png)
. В пределе, при

будет заполнена вся плоскость. Для примера вот два графика для различных

.
Во-первых, здесь "начало" окружности отображается в начало координат, а "конец" в бесконечность, т.е. отображение в этой точке разрывно. Во вторых, то, что у начала координат есть прообраз, уже само по себе проблема.
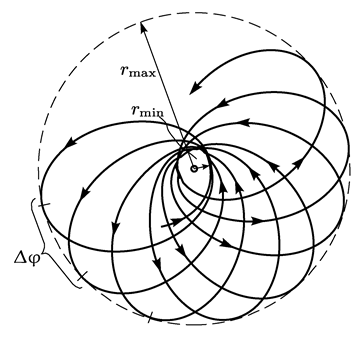
2. Рассмотрим движение массивной точки в центральном поле. Подбирая параметры системы определенным образом можно добиться того, что, во-первых, область, в которой движение разрешено, будет иметь две границы

и

, и, во-вторых, за время, в течение которого

изменяется от

до

и обратно до

, радиус-вектор повернется на угол
не равный рациональной части от

. Тогда траектория движения будет незамкнута и за бесконечное время заполнит все пространство между

и

(см. рисунок). Таким образом можно задать биекцию между полупрямой

и кольцом (с границами). Между кольцом (только вот уже без границ) и плоскостью с выколотым началом можно задать биекцию очевидным образом (отображение почти такое же как в пункте 1 для

).
Здесь снова те же проблемы. Во-первых, проблема в том, что отображение окружности в кольцо затрагивает границы кольца. Во-вторых, опять же начало и конец окружности отображаются вообще говоря в разные точки. Вот если бы, например,
было бесконечно малой рациональной частью от

, то в пределе траектория замкнулась бы через бесконечное время. Но это тоже не вариант.
В общем, такие вот помидоры. Буду рад любым идеям! :)



