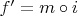делители нуля при локализации кольца

[OlgaD]

patzer2097 в сообщении #896935 писал(а):

Ну $f'$ переводит $r+\operatorname{Ker}f$ в $f(r)$, а как еще?

А точнее? Это определение слишком формально, а мне хотелось более подробнее

[olenellus]

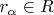
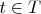
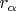
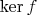
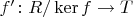
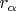
На пальцах это так: $f$ загоняет некоторые точки, напирмер $r_\alpha\in R$ в одну и ту же точку, скажем $t\in T$. Как Вы знаете, разные $r_\alpha$ в этой совокупности отличаются на элемент из $\ker f$. Отображение факторизации "слепляет" такие точки в одну. Теперь можно рассмотреть отображение $f'\colon R/\ker f\to T$, отображающая кажду точку, полученную из слепления совокупности $r_\alpha$ в соответствующую этой совокупности точку $t$. Такое отображение будет, очевидно, мономорфизмом.

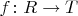
Точно так же рассуждая, строят каноническое разложение любого гомоморфизма $f\colon R\to T$ на эпиморфизм, изоморфизм и мономорфизм

$$R\overset{e}{\to}R/\ker f\overset{i}{\to}\operatorname{im} f\overset{m}{\to}T$$

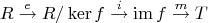
Здесь $e$ — это факторизация, а $m$ — естественное вложение. В этой схеме $f' = m\circ i$