Ваше доказательство, уважаемый ananova, очень трудно понять, потому что Вы ничего не объясняете.
Например, функция

- это функция от 2-х аргументов или от 4-ёх?
Уважаемый, Феликс Шмидель, мои объяснения могут еще больше Вас запутать, поэтому я попробую ответить на этот вопрос только.

- это функция определяющая значение

. Все значения функции равны между собой. Любые параметры, которые определены в уравнении (2.1) подходят, чтобы заменить

на новый вариант записи

. Для индексации и удобства ипользуются параметры

и

. Так удобнее выбирать любую из записей рекурсии.
Несколько сумбурно и туманно (в разных постах) можно ознакомиться еще в этой теме -
http://dxdy.ru/topic78054.htmlИмеет смысл добавить, что используется поиск противоречия (для Случая 2), известного из соотношений Барлоу (см.Рибенбойма), и записанного в уравнениях (3.2) и (3.3)
Могу еще добавить, что я где-то ошибаюсь... ;)
-- Ср ноя 27, 2013 15:53:00 --Вот уже нашел где, вместо

, надо использовать

в уравнениях (2.1) - (2.3)
(1)

(1.1)



- это функция определяющая значение

. Все значения функции равны между собой. Любые параметры, которые определены в уравнении (2.1) подходят, чтобы заменить

на новый вариант записи

. Для индексации и удобства ипользуются параметры

и

. Так удобнее выбирать любую из записей рекурсии.
(2.1)


(2.2)


(2.3)





(3.1)

Используется поиск противоречия (для Случая 2), известного из соотношений Барлоу (см.Рибенбойма), и записанного в уравнениях (3.2) и (3.3)
(3.2)

(3.3)

(4.1)

(4.2.1)

(4.2.2)


(4.3)
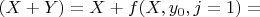

(4.3.1)

(4.4)


(Оффтоп)
PS: Не отвечайте слишком быстро - т.к. могу вносить исправления в ходе перепроверки.



