Здравствуйте, перерешиваю задания,которые не правильно решил в течение семестра, вот с этими тремя есть довольно сильные проблемы, прошу помощи.
1)доказать на основе определения измеримость функции
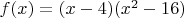
2) Интегрируема ли функция

на множестве
![$(0;1]$ $(0;1]$](https://dxdy-04.korotkov.co.uk/f/7/6/1/7611ea9b709c977d73bcf4105a4bafcc82.png)

если

принадлежит
![$(1/n;1/(n+1)]$ $(1/n;1/(n+1)]$](https://dxdy-02.korotkov.co.uk/f/9/0/f/90f8a0d541896bc73307f69701b45a6182.png)
3)Пусть множество

измеримо подмножество

. Доказать, что функция
![$f(x)=\mu(A\cap [0;x])$ $f(x)=\mu(A\cap [0;x])$](https://dxdy-03.korotkov.co.uk/f/e/a/f/eaf532c40be4cede8826178bccf668ca82.png)
непрерывно на
![$[0;1]$ $[0;1]$](https://dxdy-03.korotkov.co.uk/f/2/1/a/21ad730ee7df0b97abd700cb0f8426e682.png)
1)Тут все совсем плохо, не могу понять различия измеримой функции от ограниченной, вижу в определение измеримости какую-то ерунду в виде поточечной ограниченности
Моя идея решения заключается в следующем найти локальные экстремумы, разбить область определения на отрезочки с концами в локальных экстремумов найти в них значения, взять прообразы, а дальше не знаю...
2) тут вроде бы просто по формуле, найдем длину отрезочка

Потом составляю ряд

Сократилось

Ряд сходится, функция интегрируема, но за это задание 0 баллов, почему не понятно
3)тут вообще нет идей, пробовал использовать определения меры Лебега, связать с определением непрерывной функции, но ничиго не получилось
Помогите пожалуйста



