Ну регуляризуйте дельта-функцию в какую-нибудь узкую гауссову функцию. Ничего ж не изменится.
Кое что изменится. Как минимум изменится уровень абстракции. Это как заменить дифференциал

на конечную разность

. Я не могу объяснить это на математическом уровне строгости, попробую на "народно-хозяйственном"...

С практической, прикладной точки зрения обобщённые функции отличаются от обычных тем, что, например, принципиально не поддаются численному интегрированию "в лоб". Они, так сказать, представляют из себя абстрактную формулу, которую надо каждый раз перед использованием обрабатывать напильником прежде чем получить "число". То есть они отличаются от обычных функций, наверное, на столько же на сколько "числовые" формулы (

) отличаются от "символьных" формул (

). Находятся на более высоком уровне абстракции. Например, интеграл

в котором фигурирует обобщённая функция

есть некий, как бы, всего лишь "символ" в том смысле, что его нельзя взять численно "в лоб" вот прямо как написано. Вместо этого, прежде чем выудить из него "число", сначала надо подставить
формулу (2) в
формулу (1) и изменить порядок интегрирования: сначала брать интеграл по

, затем по

.
![$$
\psi(t, x) = \int\limits_{-\infty}^{+\infty} \left[ \cos \left(t \sqrt{m^2 + p^2} \right) \left( \frac{1}{2 \pi} \int\limits_{-\infty}^{+\infty} \cos (p (x - y)) \, \varphi(y) \, dy \right) \right] dp \eqno(3)
$$ $$
\psi(t, x) = \int\limits_{-\infty}^{+\infty} \left[ \cos \left(t \sqrt{m^2 + p^2} \right) \left( \frac{1}{2 \pi} \int\limits_{-\infty}^{+\infty} \cos (p (x - y)) \, \varphi(y) \, dy \right) \right] dp \eqno(3)
$$](https://dxdy-04.korotkov.co.uk/f/3/7/2/372332af08df28be5006ba2c0afd1e2382.png)
Только после этих символьных манипуляций с обобщённой функцией

, мы получаем формулу (3) пригодную для численного интегрирования - из неё можно получить "число".
Вот, а я о том, что если вы берёте начальное возбуждение шириной

то покажите его эволюцию на промежутке времени до

Да хоть на 20.
Но рядышком я покажу график коротковолнового возбуждения, чтоб было с чем сравнить.
Сравнение эволюции пакетов с

и

на больших временах (

,

,

,

,

комптоновских времён):
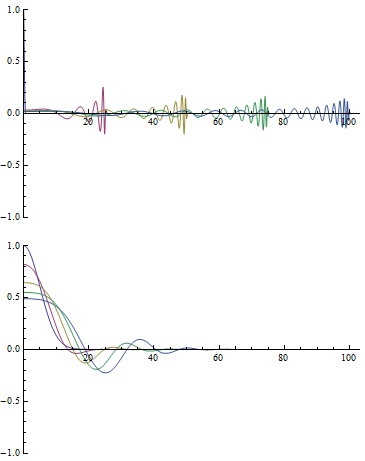
Коротковолновое возбуждение с

за 100 комптоновских времён убежало на расстояние примерно 100 комптоновских длин, то есть распространялось примерно со скоростью света.
Длинноволновое возбуждение с

за 100 комптоновских времён (или за 20 своих исходных длин делённых на скорость света) кончиком хвоста едва доползло до

50 комптоновских длин, а его "центр тяжести" едва сдвинулся на

15 комптоновских длин (или на

3 своих изначальных).



