Некоторые св-ва последо-стей на огран.интерв.натурально ряда

[vicvolf]

Полученные в работе формулы для определения плотности рассмотренных последовательностей на интервале [$2, x$) можно использовать для получения оценок количества членов этих последовательностей на данном интервале.
На основании формулы (23) для больших х получаем приближенную формулу для оценки количества членов последовательности, полученной после r-ого шага решета Эратосфена $f_r(n)$ на интервале [$2, x$):
$\pi(f_r,2,x) \approx [x \cdot \prod_{i=1}^{r} (1-1/p_i)]$.(62) с относительной ошибкой $\bar{\Delta_{or}}$, определяемой по формуле (26).
Ниже приведены значения $\prod_{i=1}^{r} (1-1/p_i)$ для различного числа шагов решета Эратосфена:
r=1 - $\prod_{i=1}^{r} (1-1/p_i) =1/2=0,5$,
r=2 - $\prod_{i=1}^{r} (1-1/p_i)=1/3=0,33...$,
r=3 - $\prod_{i=1}^{r} (1-1/p_i)=4/15=0,26....$,
r=4 - $\prod_{i=1}^{r} (1-1/p_i)=8/35=0,228571429$,
r=5 - $\prod_{i=1}^{r} (1-1/p_i)=16/77=0,207792208$,
r=6 - $\prod_{i=1}^{r} (1-1/p_i)=192/1001=0,191808192$,
r=7 - $\prod_{i=1}^{r} (1-1/p_i)=3072/17017=0,180525357$,
r=8 - $\prod_{i=1}^{r} (1-1/p_i)=55296/323323=0,171024022$,
r=9 - $\prod_{i=1}^{r} (1-1/p_i)=1216512/7436429=0,163588195$,
r=10 - $\prod_{i=1}^{r} (1-1/p_i)=34062336/315656441=0,157947223$,
r=11 - $\prod_{i=1}^{r} (1-1/p_i)=1021870610/6685349670=0,1522852232$.
Например, для $x=10^{8} , r=5$:
$\pi(f_5,2,10^{8}) \approx [10^{8} \cdot \prod_{i=1}^{5} (1-1/p_i)] =2,08 \cdot 10^{7}$.
Из формулы (26) следует, что $\bar{\Delta_{or}} } =O(1/x)$, поэтому $ \lim \limits_{x \to \infty} {\bar{\Delta_{or}} }=0$. Следовательно, для оценки количества членов последовательности, полученной после r-ого шага решета Эратосфена $f_r(n)$ на интервале [$2, x$) справедлива асимптотическая формула:
$\pi(f_r,2,x) \sim [x \cdot \prod_{i=1}^{r} (1-1/p_i)]$.(63)
На основании формулы (48) для любых х (в том числе небольших) справедлива приближенная формула для оценки количества членов последовательности, полученной после r-ого шага решета Эратосфена $f_r(n)$ на интервале [$2, x$):
$\pi(f_r,2,x) \approx r-1+[x \cdot \prod_{i=1}^{r} (1-1/p_i)]$.(64)
Расчеты показывают, что абсолютная ошибка данной формулы не превосходит 1 при r меньше 6 независимо от величины х. При $r>5$ абсолютная ошибка формулы (64) больше 1, но меньше, чем в формуле (62).
Из формулы (34) следует асимптотическая формула для определения количества членов последовательности простых чисел $f(n)$ на интервале [$2, x$):
$\pi(f,2,x) \sim [0,5e^{\gamma}x \cdot \prod_{p\leq \sqrt{x}}(1-1/p)]$,(65) которую можно использовать при больших значениях х.
На основании формулы (57) получается приближенная формула (59) для определения количества членов последовательности простых чисел $f(n)$ на интервале [$2, x$):
$\pi(f,2,x) \approx \pi(\sqrt{x})-1)+[\prod_{p \leq \sqrt{x}}(1-1/p)]$, которая дает хорошие результаты при небольших х (смотрите предыдущее сообщение).

[vicvolf]

Теперь поставим другую задачу. Определить вероятность, что наугад выбранное натуральное число из интервала [$2, x$) принадлежит указанной ниже последовательности.
Для начала рассмотрим последовательность $g_k(n)=n^k$, где n пробегает значения натурального ряда из указанного интервала, а k - постоянное натуральное число.
Количество членов в последовательности $g_k(n)$ на интервале [$2, x$) равно:
$\pi(g_k,2,x)=\lfloor \sqrt[k](x-1) \rfloor-1$.(1)
Следовательно, плотность последовательности $g_k(n)$ на интервале [$2, x$) равна:
$P(g_k,2,x)=\frac {\lfloor \sqrt[k](x-1) \rfloor -1} {x-2}$.(2)
Например, плотность натурального ряда на интервале [$2, x$) ( k=1):
$P(g_1,2,x)=\frac {\lfloor (x-1) \rfloor -1} {x-2}=1$.
Плотность последовательности $g_2(n)=n^2$ на интервале [$2, x$):
$P(g_2,2,x)=\frac {\lfloor \sqrt (x-1) \rfloor -1} {x-2}$.(2.1)
При $x\in [2,5)$ - $P(g_2,2,x)=0$, $x\in [5,10)$ - $P(g_2,2,x)=1$, $x\in [10,17)$ - $P(g_2,2,x)=2$, $x\in [17,26)$ - $P(g_2,2,x)=3$, $x\in [26,37)$ - $P(g_2,2,x)=4$...и.т.д.
Так как последовательность $g_k(n)$ является целочисленной строго возрастающей, то плотность данной последовательности на интервале [$2, x$) является вероятностью, что наугад взятое натуральное число из данного интервала принадлежит этой последовательности.
Немного напомню. В теме "Асимптотическая плотность последовательности и гипотезы о простых числах" было дано определение плотности последовательности f(n) на конечном интервале натурального ряда [A,B): $P(f,A,B)=\frac {\pi(f,A,B)} {B-A}.$ (3)
Также были доказаны утверждения.
Утверждение 1
Целочисленные строго-возрастающие последовательности на конечном интервале натурального ряда с добавлением последовательности не имеющих членов и последовательностей, имеющих один член на данном интервале образуют сигма-алгебру.
Утверждение 2
Плотности целочисленных строго возрастающих последовательностей на конечном интервале натурального ряда [A,B) (3) с добавлением последовательности не имеющих членов и последовательностей, имеющих один член на данном интервале являются значениями конечной вероятностной меры - $P(A,B)$.
На основании утверждений (1), (2) плотность последовательности простых чисел f(n) (целочисленной строго возрастающей) является значением вероятностной меры на конечном интервале натурального ряда.
Учитывая это, искомая вероятность равна:
$Pr(A_k)= P(g_k,2,x)=\frac {\lfloor \sqrt[k](x-1) \rfloor -1} {x-2}$.(4)
Асимптотическая плотность последовательности $g_k(n)=n^k$ равна:
$P^{*}(g_k.2.x) \sim \sqrt[k](x)/x=\frac {1} {x^{1-1/k}}$.(5)
Теперь определим вероятность, что наугад взятое натуральное число из интервала [$2, x$) принадлежит объединению последовательностей $\cup_{k=2}^m g_k(n)$.
На интервале [$2, x$) последовательности $g_k(n)$ не имеют общих членов, поэтому:
$Pr(\cup_{k=2}^m A_k)=\sum_{k=2}^{m} {Pr(A_k)}=\frac {\sum_{k=2}^{m}{\lfloor \sqrt[k](x-1) \rfloor -1}} {x-2}$.(6)
Например, если $x=10^{12}$, то по формуле (6):
$Pr(\cup_{k=2}^4 A_k)=\sum_{k=2}^{4} {Pr(A_k)}=10^{-6}+10^{-8}+10^{-9} \approx 10^{-6}$.
Асимптотическая плотность объединения последовательностей $g_k(n)$ на основании формулы (5) равна:
$P^{*}(\cup_{k=2}^m g_k,2,x) \sim \sum_{k=2}^{m}{\frac {1} {x^{1-1/k}}}$.(7)
Таким образом, плотность объединения последовательностей $\cup_{k=2}^m g_k(n)$. на основании (7) при больших х, примерно равна плотности последовательности $g_2(n)=n^2$ и определяется по формуле (2.1).

[vicvolf]

Рассмотрим последовательность $f_k(n)=p^k$, где р - последовательность простых чисел на интервале [$2, x$), а k - постоянное натуральное число.
Количество членов последовательности $f_k(n)$ на интервале [$2, x$) для больших х примерно равно:
$\pi(f_k,2,x) \approx \sqrt[k] {\frac {x }{\ln(x)}}$.(8)
Плотность последовательности $f_k(n)$ на интервале [$2, x$) для больших х на основании (8) примерно равна:
$P(f_k,2,x) \approx \frac {\sqrt[k] {\frac {x }{\ln(x)}}}{x} =\frac {1}{\sqrt[k] {x^{k-1}\ln(x)}}$.(9)
На основании формулы (9) плотность последовательности простых чисел $f_1(n)$ на интервале [$2, x$) для больших х примерно равна $1/\ln(x)$, что соответствует асимптотическому закону простых чисел.
Учитывая, что последовательность $f_k(n)$ является целочисленной строго возрастающей, вероятность, что наугад взятое натуральное число из интервала [$2, x$) принадлежит данной последовательности на основании формулы (9) равна:
$Pr(B_k)=P(f_k,2,x) \approx \frac {1}{\sqrt[k] {x^{k-1}\ln(x)}}$.(10)
Асимптотическая плотность последовательности $f_k$ на основании формулы (9) равна:
$P^{*}(f_k,2,x) \sim \frac {1}{\sqrt[k] {x^{k-1}\ln(x)}}$.(11)
Теперь определим вероятность, что наугад взятое натуральное число из интервала [$2, x$) (где х -большое натуральное число) принадлежит объединению последовательностей - $\cup_{k=1}^m f_k(n)$.
На интервале [$2, x$) (где х -большое натуральное число) последовательности $f_k$ не имеют общих членов, поэтому на основании (10) получим:
$Pr(\cup_{k=1}^m B_k)=\sum_{k=1}^{m}{P(f_k,2,x)} \approx \sum_{k=1}^{m}{\frac {1}{\sqrt[k] {x^{k-1}\ln(x)}}}$.(12)
Например, для $x=10^6$ вероятность, что натуральное число из интервала [$2, x$) принадлежит последовательности $\cup_{k=1}^3 f_k(n)$ на основании формулы (12) равна:

$$Pr(\cup_{k=1}^3 B_k) \approx \sum_{k=1}^{3}{\frac {1}{\sqrt[k] {x^{k-1}\ln(x)}}}=\frac {1}{6\ln(10)}+\frac {1}{10^3\sqrt {6\ln(10)}} +\frac {1}{10^4\sqrt[3] {6\ln(10)}} \approx 0,072$$

.

[vicvolf]

Определим вероятность, что наугад выбранное натуральное число из интервала [$2, x$) принадлежит объединению последовательностей - $g_1(n) \cup ... \cup g_m(n) \cup f_1(n) \cup ..\cup f_m(n)$.
Учитывая, что объединение последовательностей $g_k(n) \cup f_k(n)=g_k(n)$, указанная вероятность равна: $Pr(A_2 \cup...\cup A_m \cup B_1 \cup...\cup B_m)=Pr(B_1 \cup A_1 \cup..\cup A_m)$.(13)
Так как последовательности $f_1(n)$ (последовательность простых чисел) и $g_k(n)$, являющиеся последовательностями составных чисел, не имеют общих членов, то на основании (13) получаем:

$$Pr(A_2 \cup...\cup A_m \cup B_1 \cup...\cup B_m)=Pr(B_1 \cup A_1 \cup..\cup A_m)=Pr(B_1)+\sum_{k=2}^{m} {Pr(A_k)}.(14)$$

В сообщении от 16.01.2014 показано. что плотность объединения последовательностей $\cup_{k=2}^m g_k(n)$. на основании (7) при больших х, примерно равна плотности последовательности $g_2(n)=n^2$ и определяется по формуле (2.1).
Учитывая это, при больших х справедлива формула:
$Pr(A_2 \cup...\cup A_m \cup B_1 \cup...\cup B_m) \approx Pr(A_2)+Pr(B_1)$, (15) где $Pr(A_2) \approx \frac {1}{\sqrt {x}}$, а $Pr(B_1) \approx \frac {1}{\ln(x)}$.
Так как при больших х справедливо неравенство - $\frac {1}{\ln(x)} \gg \frac {1}{\sqrt {x}}$, то на основании (15) получаем:
$Pr(A_2 \cup...\cup A_m \cup B_1 \cup...\cup B_m) \approx Pr(A_2)+Pr(B_1) \approx \frac {1}{\ln(x)}$.(16)
По формуле (16) определяется искомая вероятность, что наугад выбранное натуральное число из интервала [$2, x$) принадлежит объединению последовательностей - $g_1(n) \cup ... \cup g_m(n) \cup f_1(n) \cup ..\cup f_m(n)$.
Следовательно, искомая величина примерно равна плотности простых чисел.

[vicvolf]

Недавно в другой теме я писал.

vicvolf в сообщении #833226 писал(а):

Важно, что N можно взять сколь угодно большим, но конечным и плотность последовательности взаимнопростых чисел на интервале натурального ряда от 1 до N будет являться вероятностью и формулу для вероятности независимых событий можно использовать с ошибкой, стремящейся к 0 с ростом N. Поэтому существует верхняя асимптотическая плотность последовательности k-взаимнопростых чисел на множестве $N^k$ и она равна $1/\zeta(k)$, где $\zeta$ - функция Римана.

Это подтверждается частично здесь http://ru.wikipedia.org/wiki/%D0%9F%D0% ... 1%80%D0%B8. А именно вероятность того, что любые три случайным образом выбранных положительных целых числа будут взаимно просты, равна $1/\zeta(3)$, в том смысле, что при $N\to\infty$ вероятность того, что три положительных целых числа, меньших, чем ${\textstyle{N}}$ (и выбранных случайным образом) будут взаимно простыми, стремится к $1/\zeta(3)$, (постоянная Апери).
Дзета-функция Римана для вещественных s > 1 больше 1, поэтому $1/\zeta(k)<1$. Кроме того, на основании свойств функции Римана, предел $1/\zeta(k)$ при $k\to\infty$ равен 1.
Пока не привожу вероятностное пространство и доказательство этого факта.

[vicvolf]

Теперь перейду к рассмотрению вероятностного пространства.
Пусть $A$ конечное множество последовательных натуральных чисел, т.е. $A={1,2,...N}$ и $k$ - целое положительное число. Обозначим $A^k$ множество всех кортежей $<x_1,...x_k>$ из $A^k$, т.е. $A^k=\{<x_1,...x_k>|x_1 \in A,...x_k \in A\}$. (1)
Иначе говоря, множество $A^k$ является $k-$ кратным прямым произведением множества $A$.
Пусть предикат $R(x_1,...x_k)$ имеет смысл для всех элементов множества $A^k$, т.е. для любого кортежа $(x_1,...x_k)$ из $A^ k$ значение предиката $R(x_1,...x_k)$ либо истинно, либо ложно.
Выделим подмножество $B \subset A^k$, состоящая в точности из тех кортежей $<x_1,...x_k>$ из $A^k$, для которых $R(x_1,...x_k)$ истинно, т.е. $B=\{(x_1,...x_k) \in A^k|R(x_1,...x_k)\}$. (2)
Пример.
$R(x_1,x_2,x_3)=(x_1+x_2=0) \cup (x_1-x_2+x_3<0)$.

Утверждение 1
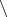
Алгебра $<\{A^k,\varnothing ,P(A^k)\},\cup ,\setminus>$ является алгеброй событий, где $P(A^k)$ - множество всех подмножеств непустого множества $A^k$, а $\cup$, $\setminus$ - соответственно операции объединения и дополнения подмножеств.

Перед доказательством утверждения напомню определение алгебры событий.
Множество $P(C)$, элементами которого являются подмножества множества $C$, удовлетворяющее условиям:
1. Множество $P(C)$ содержит достоверное событие (множество С).
2. Вместе с любым событием (подмножеством), множество $P(C)$ содержит противоположное событие (дополняющее подмножество).
3. Вместе с любыми двумя событиями (подмножествами), множество $P(C)$ содержит их объединение.

Доказательство

Известно, что алгебра $<P(A^k),\cup ,\setminus>$ является алгеброй типа (2,1), поэтому для любых подмножеств непустого множества $A^k$, выполняются условия 2 и 3.
Множество $\{A^k,\varnothing ,P(A^K)\}$ содержит достоверное событие - $A^k$, т.е. выполняется условие 1, а также содержит противоположное для него событие (дополняющее подмножество) - $\varnothing $ и наоборот. Таким образом, для достоверного события и пустого множества также выполняется условие 2.
Объединение любого подмножества множества $A^k$ и множества $A^k$ является множеством $A^k$, а объединение любого подмножества множества $A^k$ и пустого множества $\varnothing $ является тем же подмножеством множества $A^k.$
Следовательно, все условия 1, 2, 3 для алгебры $<\{A^k,\varnothing ,P(A^k)\},\cup ,\setminus>$ выполнены и поэтому она является алгеброй событий ч.т.д.

Буду благодарен за замечания и предложения.

[vicvolf]

Напомню определение вероятностной (нормированной) меры на конечном пространстве событий.

Пусть $\Omega$ конечное множество (множество элементарных событий), $F$ - алгебра подмножеств $\Omega$ (алгебра событий).
Тогда вероятностной мерой на $(\Omega, F)$ называется функция $P$, отображающая $F$ на множество действительных чисел, обладающая следующими свойствами:
1. Для любого события $D \in F$ выполняется $P(D)\geq 0$.
2. Для любых двух событий $D_1 \in F$ и $D_2 \in F$ выполняется $P(D_1 \cup D_2)=P(D_1)+P(D_2)$.
3. $P(\Omega)=1$.

Пусть $\Omega=A^k$.
В утверждении 1 показано, что алгебра $<\{A^k,\varnothing ,E(A^k)\},\cup ,\setminus>$ является алгеброй событий, где $E(A^k)$ - множество всех подмножеств непустого множества $A^k$, а $\cup$, $\setminus$ - соответственно операции объединения и дополнения подмножеств. Таким образом, в данном случае $F=<\{A^k,\varnothing ,E(A^k)\},\cup ,\setminus>$.

Введем функцию плотности k-кортежей на множестве $B \subseteq A^k$, определяемую по формуле:
$P(B)=\pi(B)/N^k$ (3), где $\pi(B)$ - количество k-кортежей в множестве $B$.
Докажем, что $P(B)$ является вероятностной мерой на конечном пространстве событий.

[vicvolf]

Утверждение 2
Плотность k-кортежей на множестве $B \subseteq A^k$, определяемая по формуле (3) - $P(B)=\pi(B)/N^k$ является вероятностной мерой на конечном пространстве событий.

Доказательство
Свойство 1. Для любого события $D \in F$ выполняется $P(D)\geq 0$, так как $\pi(D) \geq 0$ и $N^k>0$.

Свойство 2. Для любых двух событий $D_1 \in F$ и $D_2 \in F$ выполняется $P(D_1 \cup D_2)=P(D_1)+P(D_2)$, если $D_1$ и $D_2$ не совместны.
На основании определения (3) $P(D_1 \cup D_2) =\pi(D_1 \cup D_2)/N^k$. (4)
Так как $D_1$ и $D_2$ не совместны, то соответствующие подмножества не пересекаются. Поэтому $\pi(D_1 \cup D_2)=\pi(D_1)+\pi(D_2)$ и на основании (4) $P(D_1 \cup D_2) =\pi(D_1 \cup D_2)/N^k=\pi(D_1)/N^k+\pi(D_2)/N^k=P(D_1)+P(D_2)$ (5).

Свойство 3. $P(\Omega)=1$. Если $\Omega=A^k$, то на основании (3) $P(A^k)=\pi(A^k)/N^k=N^k/N^k=1$. (6) ч.т.д.

[vicvolf]

Рассматриваемая ранее вероятностная мера целочисленной строго возрастающей последовательности на ограниченном интервале натурального ряда является частным случаем вероятностной меры последовательности k-кортежей на $A^k$, определенной в (3). Поясним это.
k-местный предикат $R(x_1,...x_k)$ является условием, накладываемым одновременно на k свободных переменных: $x_1,...x_k$, каждая из которых принимает значение от 1 до $N$.
В рассматриваемой ранее вероятностной мере условие накладывалось только на одну свободную переменную, чтобы она принимала значение из какой-либо целочисленной строго возрастающей последовательности на ограниченном интервале натурального ряда.
Например, в гипотезе Харди-Литлвуда для простых близнецов рассматривается случай, когда натуральное число x удолетворяет условию истинности предиката от одной свободной переменной: $R(x)=(x \in P) \cap (x+2 \in P)$, где $P$ - множество простых чисел.
Истинность k-местного предиката (от k сводных переменных) соответствует выполнению k независимых событий.
Например, когда предикат $R(x_1,...x_k)=(x_1 \in P) \cap ... \cap (x_k \in P)$ является истинным.
Условие истинности k-местного предиката соответствует следующей вероятностной модели.
На шарах надписываются номера от 1 до $N$ и они укладываются в урну. Далее из урны поочередно наугад выбираются шары. Сначала выбирается первый шар, записывается его номер $x_1$ и обратно укладыватся в урну. Затем также выбирается второй шар, записывается его номер $x_2$ и обратно укладывается в урну и.т.д. до $k$ -ого шара включительно. После этого проверяется выполнение условия истинности k местного предиката $R(x_1,...x_k)$ для полученного $k$ кортежа $(x_1,...x_k)$.
Если бы шары не возвращались в урну, то не была бы реализована независимость событий, так как не был бы возможен случай повторения значений: $x_1=x_2=...=x_k$.
Определим плотность k-кортежей для случая повторения значений по формуле (3):
$P(x_1=x_2=...=x_k)=N/N^k=1/N^{k-1}$. (7)
Рассмотрим еще один пример нахождения плотности k кортежей для случая истинности предиката $R(x_2>x_1)$:
$P(x_2>x_1)=(N^2-N)/2N^2=1/2(1-1/N)$. (8)

[vicvolf]

Известно, что k-арное отношение $R$ - это множество k-кортежей $<x_1,...x_k> \in R$, которое является подмножеством прямого произведения $A^k$.
Напомню, что k-арное отношение является рефлексивным на множестве $A$, если для любого $x \in A$ выполняется $<x,...x> \in R$.
Назовем главной диаганалью прямого произведения $A^k$ k-кортежи $<x_1,...x_k>$, удолетворяющие условию $<x_1=...=x_k> \in R$.
Отсюда следует, что рефликсивному k-арному отношению принадлежит главная диаганаль множества $A^k$.
Пример рефлексивного k-арного отношения:
$<x_1 \leq x_2 \geq x_3> \in R$.
Известно, что k-арное отношение является антирефлексивным на множестве $A$, если для любого $x \in A$ выполняется $<x,...x> \notin R$.
Отсюда следует, что рефликсивному k-арному отношению не принадлежит главная диаганаль множества $A^k$.
Пример антирефлексивного k-арного отношения:
$<x_1 > x_2 < x_3> \in R$.
Напомню, что бинарное отношение $R$ на множестве $A$ называется симметричным на $A$, если для любых $x_1 \in A, x_2 \in A$ из $<x_1,x_2> \in R$ следует, что $<x_2,x_1> \in R$.
Обобщим это свойство. k-арное отношения $R$ на множестве $A$, если для любых $x_1 \in A, ...x_k \in A$ из $<x_1,...x_k> \in R$
следует, что $(<x_2,x_1,...x_k> \in R) \cap...\cap (<x_k,x_1,...x_k> \in R)$, т.е $R$ принадлежат все перестановки $x_i$.
Таким образом, для симметричного k-арного отношения кортежи $<x_1,...x_k> \in R$ расположены симметрично относительно главной диаганали.
Примером симметричного k-арного отношения является отношение между k взаимнопростыми числами. На основании указанной выше вероятностной модели - проверяется условие, что номера k последовательно вынутых шаров (с возвратом) окажутся взаимнопростыми числами.
Назовем k-арное отношение $R$ на множестве $A$ антисимметричным, если для любых $<x_1 \in A, ...x_k\in A >$ из $<x_1,...x_k> \in R$
следует, что $(<x_2,x_1,...x_k> \notin R) \cup...\cup (<x_k,x_1,...x_k> \notin R)$.
Таким образом, для антисимметричного k-арного отношения для кортежа $<x_1,...x_k> \in R$ нет симметричного относительно главной диаганали и сама главная диаганаль не принадлежит $R$.
Пример несимметричного k-арного отношения:
$R(x_1,...x_k)=(x_1>x_2) \cap...\cap (x_{k-1}.x_k)$.
Указанные выше свойства k-арных отношений помогают в определении вероятности по формуле (3).
Например, формула (8) получается, как количество точек, имеющих натуральные значения в $A^2$ , т.е. $N^2$, за вычетом точек, находящихся на главной диаганали - N и деленное попалам, так как нас интересуют только точки, находящиеся над главной диаганалью.

[vicvolf]

Небольшое исправление.
Пример несимметричного k-арного отношения:
$R(x_1,...x_k)=(x_1>x_2) \cap...\cap (x_{k-1}>x_k)$.

Теперь продолжу.
Рассмотрим также асимптотическую плотность k-кортежей на множестве $B \subseteq A^k$, определяемую по формуле:
$P'(B)=\lim \limits_{N \to \infty} {\frac {\pi(B)} {N^k}}$.(9)
Для асимптотической плотности (9) выполняются свойства 1-3 плотности, введенной по формуле (3), но не выполняется свойство счетной аддитивности, необходимое чтобы асимптотическая плотность (9) являлась вероятностной мерой на бесконечном пространстве событий.
Обозначим $B_N$ множество $B$ при фиксированном значении $N$, а $\pi(B_N)$- количество K-кортежей $<x_1,...x_k>$ на множестве $B_N$.
В силу определения последовательность $\pi(B_N)$ является неубывающей.
Рассмотрим 3 случая данной последовательности.
1. Последовательность $\pi(B_N)$, начиная с некоторого $N_0$ не возрастает, т.е. остается постоянной величиной.
В этом случае $P'(B)=\lim \limits_{N \to \infty} {\frac {\pi(B_N)} {N^k}}=0$.
2. Последовательность $\pi(B_N)$ возрастает неограниченно, как $O(N^s)$, где $s<k$.
В этом случае $P'(B)=\lim \limits_{N \to \infty} {\frac {\pi(B_N)} {N^k}}=0$.
Пример для случая 2 - (7).
3. Последовательность $\pi(B_N)$ возрастает неограниченно, как $O(N^s)$, где $s=k$, но $\pi(B_N) \leq N^k$.
В этом случае $P'(B)=\lim \limits_{N \to \infty} {\frac {\pi(B_N)} {N^k}}=a$, где постоянная $a\leq 1$.
Пример для случая 3 - (8). В этом случае асимптотическая плотность равна 1/2.

Приведу еще пример для случая 2.
Пусть из последовательности натуральных чисел: $1,2,...N$ наугад выбираются k-чисел $k<N$, притом числа могут повторяться.
Определить асимптотическую плотность (9) простых k-кортежей, т.е что все выбранные числа окажутся простыми.
На основании асимптотического закона простых чисел значение $\pi(B_N)=N^k/\ln^k(N)$, поэтому из (9) получаем:
$P'(B)=\lim \limits_{N \to \infty} {\frac {\pi(B_N)} {N^k}} =\lim \limits_{N \to \infty} {\frac {N^k/\ln^k(N)} {N^k}}=0$.
Интересно, что асимптотическая плотность (9) для k-кортежей взаимнопростых чисел относится к случаю 3 и не равна 0, как для простых чисел, т.е. их плотность значительно больше. Этот пример рассмотрим далее.

[vicvolf]

Рассмотрим пример для случая 3.
Пусть из последовательности натуральных чисел: $1,2,...N$ наугад выбираются k чисел $k<N$, притом числа могут повторяться.
Определить асимптотическую плотность (9) для k-кортежей взаимнопростых чисел, т.е что выбранные k чисел окажутся взаимнопростыми.

Введем следующие обозначения:
- $C_i$ - событие, что выбранное наугад i-ое натуральное число кратно натуральному числу d;
- $C$ - событие, что наибольший общий делитель (НОД) для выбранных k чисел - $x_1,...x_k$ равен d или $gcd (x_1,...x_k)=d$;
- $D$ - событие, что $gcd (x_1/d,...x_k/d)=1$.
Тогда, учитывая, как было показано выше, что плотность (3) является вероятностью и независимость событий в выборке, получим:
$Pr(C)=Pr(D) \cdot \prod_{i=1}^k Pr(C_i)$, (10) где $Pr(A)$ - вероятность события $A$.
Естественно натуральные числа, кратные d принадлежат последовательности $f(n)=dn$. Как было показано ранее (в начале темы), плотность данной последовательности на ограниченном интервале натурального ряда от 1 до N, где N- большое натуральное число $(N \gg d)$, достигает максимума при $N=dn$ (n - натуральное число) равного $1/d$. Плотность последовательности $f(n)=dn$ на ограниченном интервале натурального ряда от 1 до N достигает своего минимума при $N=dn+(d-1)$ равного $\frac {1} {d+[\frac {d-1} {N/d}]}$.
На основании формулы (5) (начало темы) отклонение плотности последовательности $f(n)=dn$ на ограниченном интервале натурального ряда от значения $1/d$ не превосходит $1/N$.
Таким образом, справедливо $Pr(C_i)=1/d+O(1/N)$. (11)
Из (11) вытекает $\prod_{i=1}^k Pr(C_i)=1/d^k+O(1/N)$. (12)
Учитывая, что $\sum_{d=1}^{\infty}{Pr(C)}=1$ на основании (10) и (12) получим:
$Pr(D) \cdot \sum_{d=1}^{\infty}{(1/d^k+O(1/N))}=1$.(13)
Следовательно, $Pr(D)=1/(\sum_{d=1}^{\infty}{(1/d^k+O(1/N))})$. (14)
С другой стороны, (14) является плотностью k-кортежей взаимнопростых чисел на ограниченном интервале натурального ряда от 1 до N - $P(D)$.
Поэтому на основании (14) искомая асимптотическая плотность последовательности k-кортежей взаимнопростых чисел равна:

$$P'(D)=\lim \limits_{N \to \infty} {P(D)}=\lim \limits_{N \to \infty} {1/(\sum_{d=1}^{\infty}{(1/d^k+O(1/N))})}=1/\sum_{d=1}^{\infty}{1/d^k}=1/\zeta(k),(15)$$

где $\zeta$ - функция Римана.

Буду благодарен за замечания и предложения.

[vorvalm]

vicvolf в сообщении #842649 писал(а):

Пусть из последовательности натуральных чисел: $1,2,...N$ наугад выбираются k чисел $k<N$, притом числа могут повторяться.
Определить асимптотическую плотность (9) для k-кортежей взаимнопростых чисел, т.е что выбранные k чисел окажутся взаимнопростыми.

Разве повторяющиеся числа могут быть взаимно простыми?

[vicvolf]

Не могут. Здесь просто говорится в условиях выборки, что в качестве k-кортежей могут выбираться любые натуральные числа от 1 до N, в том числе повторяющиеся.

[vicvolf]

vicvolf в сообщении #842649 писал(а):

асимптотическая плотность последовательности k-кортежей взаимнопростых чисел равна:

$$P'(D)=1/\sum_{d=1}^{\infty}{1/d^k}=1/\zeta(k)$$

где $\zeta$ - функция Римана.

Уважаемые участники форума!
Кто-нибудь из Вас встречал это утверждение с доказательством ранее? Если да, то при возможности дайте на него ссылку. Я не нашел.

Буду очень благодарен.