Нашел подобный
пример, там не делят на два решения.
В первом решении под корнем стоит выражение

. Здесь мы можем не делить на случаи
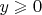
и

, поскольку первый случай получается при

, а второй — при

.
Второе решение просто некорректно, так как потеряны решения, в которых

.
Не надо брать пример с плохих образцов.
Оставлю как есть, в общем.
И потеряете все решения, в которых

.
И, получается, интеграл уравнения будет зависеть от значения


Экая невидаль! Решение вполне может выражаться разными формулами в разных областях.



