Это приводит к путанице с единицами измерения. Стоит ли запоминать такой подход?
Путаницы нет. Просто вы "переселяетесь" в другой мир, геометрический, с другой системой размерностей.
Раньше было:
длина -

время -

скорость -

ускорение -

геометрический угол -

геометрическая кривизна линии -

(кривизна - это

где

- радиус кривизны)
Теперь стало:
длина -

время -

скорость -

ускорение -

геометрический угол -

геометрическая кривизна линии -

и видно, что геометрически длина и время - это длины в пространстве-времени; скорость - это угол в пространстве-времени - безразмерная величина; а ускорение - это, по сути, кривизна мировой линии в пространстве-времени, и поэтому имеет размерность обратной длины, как кривизне и положено.
Но если у нас появилась величина в размерности

как с ней быть? Она соответствует целому набору "старых" размерностей:





и вообще

для любых

Но какой именно? А тут надо решать, глядя на физический смысл той величины, которую мы вычисляли. Никаких проблем в этом нет: "старые" размерности тоже сообщали не всю информацию о величине, и надо было отдельно решать, то ли это длина, то ли расстояние, то ли пройденный путь, и т. п. Зато теперь эта размерность сообщает нам о том, что у нашей величины есть несколько "родственников", отличающихся от неё всего лишь по тому, как они ориентированы в пространстве и во времени.
Теперь посмотрим на размерности динамических величин. Раньше у нас было:
масса -
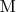
импульс -

энергия -

сила -

мощность -

плотность массы -

плотность импульса, поток массы -

давление (поверхностная плотность силы), плотность энергии, поток импульса -

поток энергии -

Теперь стало:
масса -
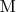
импульс -
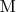
энергия -
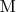
сила -

мощность -

плотность массы -

плотность импульса, поток массы -

давление (поверхностная плотность силы), плотность энергии, поток импульса -

поток энергии -

и снова у нас величины, родственные в пространственно-временном смысле, оказываются одинаковой размерности.
Есть один 4-вектор в пространстве-времени, и это 4-вектор энергии-импульса. Совершенно логично, что его компоненты имеют одинаковые размерности, и совпадают по размерности с длиной, хотя называются они (по старой традиции) импульсом и энергией, а его длина - массой.
Все плотности и потоки в пространстве-времени совпадают по размерности, потому что плотность - это геометрический поток через площадку, ориентированную поперёк оси времени, а поток - это такой же геометрический поток через площадку, ориентированную вдоль оси времени (то есть, сколько-то величины, прошедшей через заданную площадку
за единицу времени). От ориентации площадки, по геометрическому смыслу, не должна меняться размерность - вот она и не меняется. Более того, теперь совершенно естественно рассматривать площадки, ориентированные
как угодно, под любыми углами, и всё это будет давать совершенно осмысленные величины очевидных размерностей. В "старых" размерностях для таких величин даже придумать размерность было бы сложно.



