Находясь под впечатлением, какой я дурак, решил погуглить, оказалось, что на этом же форуме уже был пример рассуждений, аналогичных моим:
Есть ещё один чудик, некий Fayez A.Alhargan, так он вообще 4CT буквально в одну строку "решил". Пожалуй попробую кратко пересказать ход его мыслей.
Сначала он показывает, что если граф содержит подграф, изоморфный

с
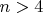
, то все, приехали, четырьмя красками не обойтись (в принципе, это очевидно). Затем пытается доказать, что у планарного графа нет и быть не может такого слишком большого полного подграфа.
Делает он это примерно так. Пусть у графа есть

вершин,

ребер и

граней. Fayez замечает, что каждая страна на проблемной карте имеет как минимум три соседа, т.е., у каждой грани графа контурной карты (дуального графу соседства) имеется как минимум
три ребра, что с учетом соответствия каждого ребра куску границы между максимум
двумя странами приводит к неравенству

, которое вместе с формулой Эйлера

дает ещё одно неравенство

(это известный результат для планарных графов, популярное изложение см. например в А.Ю.Ольшанский, Плоские графы, СОЖ, №11, 96г.).
Теперь Fayez подставляет в это неравенство значение

для полного графа, которое может быть получено из комбинаторных соображений; именно, для

число

(количество ребер) равно

, т.е., количеству единиц над главной диагональю

матрицы забитой единицами. Подстановка в ранее полученную формулу дает квадратное неравенство

, которое имеет решение
![$n\in[3;\ 4]$ $n\in[3;\ 4]$](https://dxdy-04.korotkov.co.uk/f/3/4/7/347d0289472aa6325a062d56a3e8e99a82.png)
. Из этого результата сразу же и делается вывод о несуществовании у планарного графа более чем 4-вершинного полного подграфа (точнее говоря, вывод о неукладываемости

, что почти тоже самое). :)
Хм, неужели действительно из последнего вывода следует 4-раскрашиваемость карты? Интуитивно, да, если потребовалась пятая краска при оптимальном раскрашивании полит. карты, значит текущая страна граничит с четырьмя другими, на которые уже растрачена 4-палитра, т.е, с четырьмя странами, граф соседсва для которых полный. Но ведь это не исключает существования какого-нибудь иного сценария неэкономичного использования красок... В общем, мне почему-то кажется, что здесь есть какая-то логическая проблема (типа импликации в одну сторону вместо эквивалентности)... Иначе, какого [вырезано] вокруг 4CT было столько шумихи и горы сгенерированной компьютером макулатуры? :)
Не я один такой, оказывается.
Это утешает.



