Помогите разобраться с решением задачи по теории вероятностей с элементами комбинаторики.
Задача.Пять друзей живут вместе. Они решили, что утром они будут тянуть жребий — кому из них пойти в магазин, чтобы купить к завтраку свежего хлеба. На одной из пяти бумажек будет стоять буква «x» и тот, кто вытянет талон с этой буквой, должен идти за покупкой.
Для кого из друзей вероятность вытянуть талон «х» будет наименьшей:
для того, кто тянет жребий первым, вторым, третьим, четвертым или пятым?
Решение.Исходом здесь следует назвать любую из
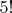
перестановок 5 (талонов). Найдем вероятность того, что билет "x" достанется

-му по счету другу. Этому событию благоприятствуют все случаи, в которых талон "x" вытаскивается

-м по счету, а остальные четыре талона могут пояляться на любом по счету месте. Это может произойти

способами. Таким образом, вероятность вытянуть талон "x"

-му по счету другу равна
Эта вероятность не зависит от

, т. е. от того, каким по порядку очередности вытягивать жребий, так что последний в очереди имеет такую же вероятность вытянуть жребий, как и первый.
У меня такой вопрос: почему здесь учитываются перестановки? Ведь тут всего лишь два типа талонов: один с "x", а остальные без. То есть не понятно, почему исход
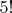
перестановок и почему 4 других талона могут вытянуться

способами.
Задача взята из книжки Колмогорова, Журбенко, Прохорова "Введение в теорию вероятностей".



