Ну вот пусть в точке

находится источник светового сигнала, в точке

— приёмник, в точке

- Вы лично. Пусть расстояние между

и

равно

, точка

— середина отрезка

,

, расстояние между

и

равно

. Скорость света считаем равной

, моменту испускания сигнала в точке

соответствует время
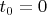
.
Расстояние от

до точек

и

по теореме Пифагора равно

(результат округлён до целого числа километров).
Информацию о том, что сигнал отправился из точки

, Вы получите в момент

информацию о прибытии его в точку

— в момент

в точку

— в момент

Таким образом, Вы
увидите, что сигнал прошёл первую половину пути за

а вторую — за
 Задача.
Задача. Пусть при тех же условиях сигнал, испущенный в точке

, имеет длительность

. Подсчитайте, какую Вы
увидите длину луча
а) в тот момент, когда Вы увидите окончание сигнала в точке

;
б) в тот момент, когда Вы увидите приход начала сигнала в точку

;
в) в тот момент, когда Вы увидите прохождение середины сигнала через точку

(предположим, что эта середина отмечена яркой вспышкой). Будет ли середина сигнала видна на одинаковых расстояниях от начала и конца сигнала?



