Одного вектора, чтобы получилось подпространство, мало — если сложить его с началом координат, получится одна точка
с чем с чем надо сложить вектор чтоб получить точку? .

С точкой же.
Началом координат, что я и написал. И вы сами это знаете, раз писали после этого определение системы координат. И потом написали совершенно то же, что и я, хотя я, может быть, написал не совсем однозначно (но вроде нет).
а что, скажем, число 1 как элемент множества действительных чисел, и число 1 как элемент множества комплексных чисел это разные вещи?
Это зависит от того как их определять, хотя в любом случае поле комплексных чисел содержит подполе, изоморфное полю вещественных (и соответствующие единицы переводятся одна в другую этим изоморфизмом). Обычно строят

, потом

на его основе, потом очевидно

.
Впрочем, тут уже столько объясняющих собралось, что им сначала между собой договориться надо, и всё равно будет "у семи нянек дитя без глаза".
+1.
Обычное
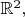
как раз, не аффинное, а векторное.
И векторное, и аффинное, и евклидово векторное, и много какое. И поле, будь понято как

.

Пусть есть множество упорядоченных пар

. Вопрос: является ли это множество векторным пространством? Сперва подумайте, а потом смотрите ответ.
(Оффтоп)
Нет, потому что не определено, как складывать элементы этого множества и как умножать их на число. И на какое число.
Определено ли что-то или нет нами, не меняет истинности никаких выводов. И ведь именно поэтому векторное пространство — не одно только какое-то

, а

. Хотя вольностью речи можно утащить поле и операции в контекст, об этом не надо забывать; и, по-моему, не стоит так, как выше, писать — можно сложить впечатление, что количество известных операций и множеств что-то меняет в их свойствах.