Итак, если же сфере либо шар не заземлены и заряжены, то, как я понял, получается следующее:
Потенциал шара есть:

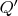
- фиктивный заряд, расположенный в центре шара.
Только как же объяснить, - почему именно в центре, так удобнее?
Снова ерунда какая-то. Вы почему-то к правильному ответу пристраиваете какую-то неправильную формулу вначале, а потом ставите между ними значок

Кто вас научил делать такую глупость? Два раза!!!
Потенциал шара
нельзя вычислить простой формулой, в которую входит непосредственно буква

Потому что этот заряд

распределён по шару очень сложно. Зато, его можно разложить на два заряда,

и

и вот тогда потенциал шара будет вычисляться просто (заметьте, это опять вычисление
не в центре, а на поверхности шара):

Здесь формула

следует просто из аддитивности заряда, а расположение (фиктивного точечного)
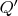
в центре - из того, что именно это расположение даст эквипотенциальное поле на поверхности шара. А теперь, из того факта, что

мы специально подобрали, следует, что сумма первых двух слагаемых равна нулю, то есть:

Как видите, величины

здесь в левой части не фигурирует.
Только как же объяснить, - почему именно в центре, так удобнее?
Не в центре, выбросьте ваши ошибочные выдумки! И не надо будет их объяснять.
И правильно ли я понял, что одновременно с
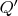
внутри шара будет располагаться ещё один фиктивный заряд

?
Да, будут два фиктивных заряда:
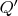
в центре шара (в данном случае - в центре, потому что только тогда потенциал, создаваемый этим зарядом, на поверхности шара постоянен), и
 не в центре
не в центре (по той причине, что потенциал этого заряда
в сумме с потенциалом внешнего заряда 
будет, по-прежнему, на поверхности шара постоянен).
И для чего вообще использовать именно два заряда-изображения в этом случае, а не один как в предыдущем?
Для того, что одним точечным зарядом величины

нельзя сделать равным потенциал на поверхности шара, где бы в пространстве вы этот точечный заряд ни расположили. Можете проверить прямым вычислением.
Мне не ясно также, почему в вышенаписанной формуле отсутствует потенциал второго фиктивного заряда?

Потому что формула до бредовости неправильная.



