А что с многогранниками в четырёх и пяти измерениях, сколько их?
Начиная с размерности 5 есть лишь три правильных многогранника: симплекс("тетраэдр"), куб и кокуб("октаэдр").
Связано это со строениями систем корней. А именно. Правильный многогранник определяется своей группой симметрии. Группа симметрии многогранника порождается отражениями. Вот мы и пришли к группе Вейля и системам корней.
Вот про графы Кокстера, характеризующие системы отражений:
http://en.wikipedia.org/wiki/Coxeter%E2%80%93Dynkin_diagramИз них не все достойны порождать симметрии многогранников(более того, не все из них даже соответствуют какой-то конечной группе отражений), а лишь

. Циферка при них это, в общем-то, размерность пространства, в котором они действуют.

-- правильный m-угольник на плоскости,

-- симплекс("тетраэдр"),

-- куб и кокуб("октаэдр")(разворот графа Кокстера соответствует двойственному многограннику, так что симметричные графы порождают самодвойственные, как тетраэдр, а несимметричные -- пары двойственных),

-- додекаэдр и икосаэдр,
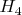
и
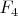
-- ещё три в четырёхмерии.
Рекомендую доступную книжечку Смирнова "Группы отражений и правильные многогранники".



