Доброго Всем времени суток! Помогите решить, пожалуйста, следующую задачу:
Заряженная бусинка может свободно скользить по тонкой спице, расположенной по диаметру кольца, равномерно
заряженного одноимённым с бусинкой зарядом. Найти период малых колебаний бусинки относительно
положения равновесия.
Известно, что заряд бусинки -

, а заряд кольца с радиусом

-

.
Вот мой неоконченный вариант решения:
Положим, что бусинку отклонили от положения равновесия на расстояние

от центра кольца. Пусть также

- угол, который составляет радиус,
проведённый в произвольную точку на кольце, со спицей, а

- отрезок, соединяющий бусинку всё с той же точкой на кольце (см. рисунок).
Тогда со стороны этого малого "кусочка" кольца с зарядом

на бусинку будет действовать сила

.
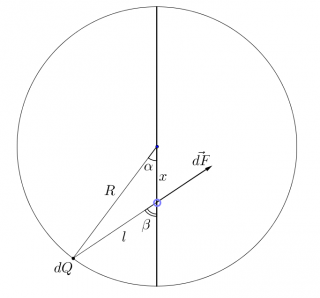
Итак, из простых геометрических соображений следует:
![$$\begin{cases}R^{2}+x^{2}-2Rx\cos{\alpha}=l^{2}\\ R/ \sin{\beta}= l/ \sin{\alpha}\\ \end{cases} \Rightarrow \begin{cases}l=\sqrt{R^{2}+x^{2}\cos{2\beta}-|\cos{\beta}|\sqrt{R^{2}-x^{2}\sin^{2}{\beta}}}, \alpha \in [0;\pi/2];\\l=\sqrt{R^{2}+x^{2}\cos{2\beta}+|\cos{\beta}|\sqrt{R^{2}-x^{2}\sin^{2}{\beta}}}, \alpha \in [\pi/2,\pi] .\\\end{cases}$$ $$\begin{cases}R^{2}+x^{2}-2Rx\cos{\alpha}=l^{2}\\ R/ \sin{\beta}= l/ \sin{\alpha}\\ \end{cases} \Rightarrow \begin{cases}l=\sqrt{R^{2}+x^{2}\cos{2\beta}-|\cos{\beta}|\sqrt{R^{2}-x^{2}\sin^{2}{\beta}}}, \alpha \in [0;\pi/2];\\l=\sqrt{R^{2}+x^{2}\cos{2\beta}+|\cos{\beta}|\sqrt{R^{2}-x^{2}\sin^{2}{\beta}}}, \alpha \in [\pi/2,\pi] .\\\end{cases}$$](https://dxdy-04.korotkov.co.uk/f/7/9/c/79c983c7ed9309c83ffcd23f894cbaa182.png)
А далее, на мой взгляд, начинается самое сложное в этой задаче.
Рассмотрим суммарную силу, действующую на бусинку со стороны кольца: она складывается из двух составляющих

(для
![$ \alpha \in [0;\pi/2]$ $ \alpha \in [0;\pi/2]$](https://dxdy-03.korotkov.co.uk/f/6/e/c/6ec68e41de556350db058aded471c1c382.png)
) и

(для
![$\alpha \in [\pi/2,\pi] $ $\alpha \in [\pi/2,\pi] $](https://dxdy-04.korotkov.co.uk/f/3/a/0/3a0e5404d230b377d99a2cafc2933aea82.png)
).
Именно так самая разница

толкает бусинку к положению равновесия.
Итак, очевидно, что:

И если верно то, что

,тогда:

Пока остановлюсь. Верно ли всё то, что написано мною выше? Уважаемые форумчане, помогите. Заранее спасибо.



