Можно ли отождествлять квантовую систему с индивидуальной реальной системой? Т.е. можно ли утверждать, что состояние индивидуальной реальной системы в определённый момент времени характеризуется статистическим оператором?
Да, можно.
Рассмотрим пример. Пусть имеется одномерная система с координатой
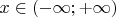
. Потенциальная энергия
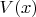
при
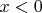
равна

, при
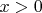
равна

(причём
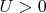
,
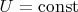
).
Пусть квантовая частица летит в положительном направлении оси

в области
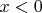
с полной энергией

(причём
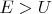
). Если частица преодолевает скачок потенциала, то она продолжает движение при
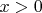
в том же направлении. Если частица не преодолевает скачок потенциала, она отражается от точки

и летит в отрицательном направлении оси

в области
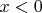
. Найти, с какой вероятностью частица преодолеет скачок потенциала, и с какой вероятностью отразится от него.
Для решения этой задачи составляется волновая функция, являющаяся решением стационарного уравнения Шрёдингера:
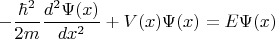
Берётся такое решение этого уравнения:
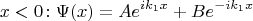
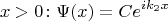
где

,

,

- некоторые комплексные числа, при которых:
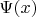 и
и  непрерывны в точке
непрерывны в точке  ,
,
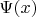 не равна тождественно
не равна тождественно  ;
;
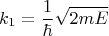
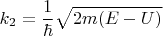
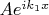
(
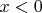
) соответствует падающей частице.
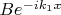
(
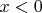
) соответствует отражённой частице.
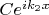
(
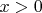
) соответствует прошедшей частице.
В точке

функция
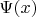
и её первая производная по

непрерывны, откуда получаем уравнения:
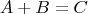
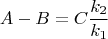
Из этих уравнений получаем:
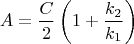
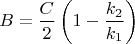
Поток вероятности выражается через волновую функцию в одномерном случае по формуле:
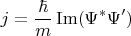
где звёздочка обозначает комплексное сопряжение, штрих - производную по координате.
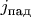
- поток падающих частиц (ему соответствует функция
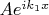
для
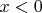
).
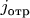
- поток отражённых частиц (ему соответствует функция
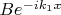
для
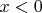
).
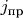
- поток прошедших частиц (ему соответствует функция
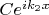
для
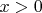
).
Для упрощения формул будем использовать обозначения:
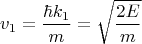
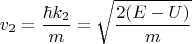
Получаем выражения для этих потоков, применяя указанную формулу к функции, соответствующей потоку:
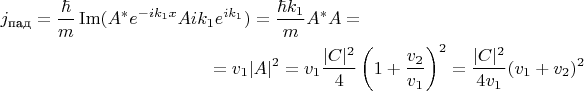
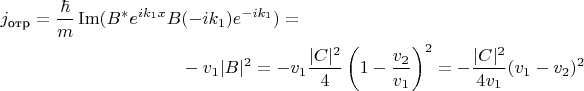
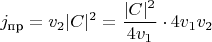
Коэффициенты пропускания и отражения выражаются через потоки:
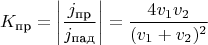
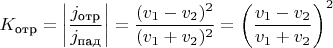
На этом данная простенькая задача решена, и тут возникают вопросы:
Из каких постулатов следует, что данную задачу следует решать именно так?
Что обозначает волновая функция
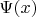
в данной задаче? Состояние индивидуальной системы в некоторый момент времени?



