http://chromotopy.org/?p=117
Прочитал данную статью и хочу поделиться интересными выводами.
В статье говорится, что так как для последовательности

, где k от 0 до p-1, асимптотическая плотность на интервале от 2 до x равна

и для второй последовательности

, где l от 0 до q-1, асимптотическая плотность на интервале от 2 до x равна

, то для взаимнопростых p и q выполняется

. Естественно это выполняется также, когда p и q простые числа. Следовательно, остатки от деления натурального числа x на различные простые числа независимы для асимптотической плотности. Напомню, что асимптотическая плотность не обладает свойством счетной аддитивности, поэтому не является вероятностной мерой.
Как уже говорилось мной ранее остатки от деления большого натурального числа x на разные простые числа зависимы для конечной плотности, являющейся вероятностной мерой, что следует из формулы Мертенса. Немного повторюсь по случаю.
На основании следствия 2 вероятность, что натуральное число х является простым равна:

Используя формулу Мертенса можно записать:

где C-постоянная Эйлера.
Это эквивалентно:

Пусть

- событие, что большое натуральное число n является простым, т.е. не делится на все простые числа меньше n.
Тогда на основании формул (1),(2):

Для больших n данная зависимость также подтверждается следующим интересным вероятностным анализом.
Чтобы число

было простым, оно не должно делиться на предыдущие простые числа. Если считать факты делимости на разные простые числа независимыми, то получаем

(здесь и далее все произведения берутся по простым числам).
Для

, малых по сравнению с

, независимость действительно хорошо соблюдается:

, а

.
Для  , сравнимых с
, сравнимых с 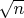 и еще больших, ситуация намного хуже:
и еще больших, ситуация намного хуже:  , а
, а  .
.Следовательно, остатки от деления большого натурального числа n на различные простые числа p действительно зависимы и отношение вероятностей, что большое натуральное число n является простым с учетом зависимости и без учета зависимости на основании (3) равно

где С- постоянная Эйлера. Сравнение с реальными данными показывает, к каким неверным выводам можно придти при подходе через асимптотическую плотность.