Возможно. Один из способов Вам назвали. Другой: записать всю конструкцию в виде экспоненты и работать с этим.
Проблема, на самом деле, одна: Ваша функция не определена при близких к

, но меньших его, значениях

. Зато определена в достаточно малой правой окрестности

. Поэтому имеет смысл считать только предел при
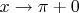
.