Бесконечность пар простых чисел-«близнецов» доказана?

[Nilenbert]

Уже до 43 миллионов снизили:

http://sbseminar.wordpress.com/2013/05/ ... 640-apart/

[shwedka]

Интересные подробности о Жанге
Back to 1999, two of Zhang’s schoolmates (and actually students back to college), Prof. Ge and Prof. Tang met by accident and talked about losing connection with Zhang. They decided to help him. The finally located him in a Subway restaurant somewhere in the South and were surprised that Zhang hadn’t give up on math at all. Imagine you were served in Subway by a guy full of world class math problems in mind secretly.
Prof. Ge works for UNH and helped to get a part-time teaching job for Dr. Zhang. Dr. Zhang told them he was working on the problem and might get something “soon”. Dr. Zhang also got much help from the head of the Math Department of UNH, Prof. Kenneth Appel, who was a world class mathematician. Dr. Zhang was given a full time job as a lecturer. His daily work load is actually not too much more than a tenure tacked professor. It is believed that was becaus of Prof. Appel. Prof. Appel passed away in April 2013. Fortunately he learned about Dr. Zhang’s break through two days before he died. That must be a very touching moment.
Mr. Zhang’s wife lives in California (it’s not unusual for Chinese couples in US). They don’t have kid. I guess Dr. Zhang has devoted all his life to math.

Кеннет Аппель был одним из 'закрывателей' проблемы четырех красок. Можно считать, что покровительство Жангу было не меньшим вкладом Аппеля в математику.

[shwedka]

на
http://terrytao.wordpress.com/2013/06/03/the-prime-tuples-conjecture-sieve-theory-and-the-work-of-goldston-pintz-yildirim-motohashi-pintz-and-zhang/
дано подробное и понятное изложение результата Жанга, с обсуждением, за счет чего можно улучшить константу

[shwedka]

Константа Жанга снижена до 4,982,086
http://sbseminar.wordpress.com/2013/05/30/i-just-cant-resist-there-are-infinitely-many-pairs-of-primes-at-most-59470640-apart/
Непонятна ситуация с самим Жангом и его статьей. Статья, будучи принятой к печати, устарела уже сейчас, в связи с улучшением оценки в 14 раз. Более того, по инициативе Тао, на полимате организуется форум по совместному подмикроскопному разбору статьи Жанга и оптимизации оценки,
см. http://polymathprojects.org/2013/06/04/polymath-proposal-bounded-gaps-between-primes/.
Pезультаты деятельности проектов полимата ранее публиковались под псевдонимом D.H.J. Рolymath.

С учетом развивающейся истории, я как-то не слишком оптимистично гляжу на профессиональное будущее Жанга. Хотя, конечно, он человек героический.

Мне известно несколько чем-то схожих случаев в России. Чрезвычайно одаренные молодые люди не могли в условиях лелеемого советскими властями антисемитизма получить приличную позицию и были вынуждены работать в промышленности или в не относящемся к математике НИИ (один мой знакомый работал бухгалтером в совхозе), и лишь с горбачевской перестройкой сумевшие либо уехать, либо получить позицию в университете. Значительной части из них удалось восстановить свою математическую силу и получить достойные результаты. Но не всем.

[ex-math]

shwedka
Снижать константу в разы и вообще доказать ее существование, вычислив явно -- две большие разницы. Первое делают сейчас все кому не лень, второе до Жанга сделать не мог никто. По-моему, сравнительный масштаб этих достижений понятен. Жанг, а не его улучшатели, войдет в историю, как вошел Виноградов с тернарной проблемой, а вовсе не Хельфготт.

[Руст]

shwedka в сообщении #732378 писал(а):

один мой знакомый работал бухгалтером в совхозе

Не Шуру (Александр) Столина имеете ввиду. Он тоже сейчас в Швеции работает. Если не ошибаюсь, он работал в одно время в Московском совхозе, только вряд ли бухгалтером.
Привет ему.

[Nilenbert]

Да нет, как раз таки Чжана запомнят, он такие первый доказавший что $\lim \inf (p_{n+1}-p_n)<\infty$. А из последующих - запомнят только того, кто доведёт константу до двух.

[Руст]

Nilenbert в сообщении #732454 писал(а):

Да нет, как раз таки Чжана запомнят, он такие первый доказавший что $\lim \inf (p_{n+1}-p_n)<\infty$. А из последующих - запомнят только того, кто доведёт константу до двух.

Из последующих запомнят того, кто укажет принципиально новый метод, даже если он не доведет до двух, скажем только до тысячи. Методом Жанга вряд ли преодолеют миллион. Всех последователей этого метода, кроме самого Жанга, все равно забудут, даже если они преодолеют миллион.

[shwedka]

Тао сформулировал чистую аналитическую задачу, к которой сводится оптимизация Жанга.


This comment is implicit in the above post, but I thought I would highlight it again. Morally speaking, the above analysis shows that the conjecture $DHL[k_0,2]$ will hold for any natural number $k_0$ for which one can find a smooth function $g: [0,1] \to {\bf R}^+$ vanishing to order at least $k_0$ at 1 for which the inequality

$k_0 \int_0^1 g^{(k_0-1)}(x)^2 \frac{x^{k_0-2}}{(k_0-2)!}\ dx > \frac{2}{1/2 + 2\varpi} \int_0^1 g^{(k_0)}(x)^2 \frac{x^{k_0-1}}{(k_0-1)!}\ dx\ $
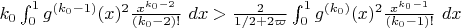
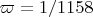
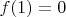
holds (with$ \varpi = 1/1158$), or equivalently if there exists a smooth function$ f: [0,1] \to {\bf R}^+$ with $f(1)=0$ such that the inequality

$(1+4\varpi) \frac{k_0(k_0-1)}{4} \int_0^1 f(x)^2 x^{k_0-2}\ dx > \int_0^1 f'(x)^2 x^{k_0-1}\ dx. (1)$

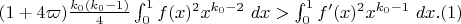
(This is cheating a little bit because there is also an error term \kappa in the analysis, but this term is exponentially small and is basically negligible for the purposes of optimising $k_0$.)

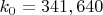
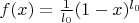
Finding the optimal value of $k_0$ for which this inequality (1) holds is a calculus of variations / numerical spectral theory / ODE problem which appears to be quite computationally tractable. Right now we can obtain the value $k_0 = 341,640$ just by substituting in monomials $f(x) = \frac{1}{l_0} (1-x)^{l_0}$, but these are not the optimal solutions and one should be able to do better, thus improving $k_0$ and hence the bound H on the gap between primes

[Руст]

shwedka в сообщении #732615 писал(а):

$(1+4\varpi) \frac{k_0(k_0-1)}{4} \int_0^1 f(x)^2 x^{k_0-2}\ dx > \int_0^1 f'(x)^2 x^{k_0-1}\ dx. (1)$

По видимому неравенство в другую сторону, потому что такому неравенству удовлетворяется любая почти постоянная функция $\frac{f'}{f}<<1$. Правда и в другую сторону
за счет выбора сильно меняющейся функции типа $\sin{\omega t, \omega >>1$ неравенство легко удовлетворяется.

Цитата:

$f(x) = \frac{1}{l_0} (1-x)^{l_0}$

Зачем множитель $\frac{1}{l_0}$, когда в обеих сторонах функции однородные второй степени относительно такого множителя?

[shwedka]

Руст в сообщении #732632 писал(а):

shwedka в сообщении #732615 писал(а):

$(1+4\varpi) \frac{k_0(k_0-1)}{4} \int_0^1 f(x)^2 x^{k_0-2}\ dx > \int_0^1 f'(x)^2 x^{k_0-1}\ dx. (1)$

По видимому неравенство в другую сторону, потому что такому неравенству удовлетворяется любая почти постоянная функция $\frac{f'}{f}<<1$. Правда и в другую сторону
за счет выбора сильно меняющейся функции типа $\sin(\omega t), \omega >>1$ неравенство легко удовлетворяется.

Цитата:

$f(x) = \frac{1}{l_0} (1-x)^{l_0}$

Зачем множитель $\frac{1}{l_0}$, когда в обеих сторонах функции однородные второй степени относительно такого множителя?

Коэффициент $\frac{1}{l_0}$, конечно, стоит для красоты. А вот про тривиальность , как стоит у Тао (в другую сторону, действительно, тривиально.)
Здесь важно точное значение коэффициента слева. В переводе на операторный язык, требование означает определенную оценку снизу для нормы оператора, задаваемого формой слева, в весовом пространстве Соболева с нормой, задаваемой интегралом справа. И такие вещи размахиванием руками не делаются, а требуют конкретного анализа.
Я считаю, что Вы не сможете провести строго анализ, который Вы очень простым называете.

[g______d]

Если я не ошибся в подсчетах, то это то же самое, что получить нижнюю оценку на первое собственное число задачи Штурма-Лиувилля

$$ -\frac{d}{dt}\left(t^{\frac{2k_0-4}{k_0-1}}\frac{dy}{dt}\right)+\lambda y,\quad y'(0)=0,\,\,y(1)=0. $$

Наверняка же это нуль какой-то спец. функции. Даже похоже что Бесселя.

[shwedka]

g______d в сообщении #732681 писал(а):

Если я не ошибся в подсчетах, то это то же самое, что получить нижнюю оценку на первое собственное число задачи Штурма-Лиувилля

$$ -\frac{d}{dt}\left(t^{\frac{2k_0-4}{k_0-1}}\frac{dy}{dt}\right)+\lambda y,\quad y'(0)=0,\,\,y(1)=0. $$

Наверняка же это нуль какой-то спец. функции. Даже похоже что Бесселя.

А откуда взяли Вы краевое условие в нуле? С таким условием, это не Бессели. Но все близко!

[g______d]

shwedka в сообщении #732685 писал(а):

А откуда взяли Вы краевое условие в нуле?

Да, там, наверное, из-за степени $t$ оно поменяется. Или вообще будет только условие регулярности?

[Руст]

shwedka в сообщении #732650 писал(а):

Руст в сообщении #732632 писал(а):

shwedka в сообщении #732615 писал(а):

В переводе на операторный язык, требование означает определенную оценку снизу для нормы оператора, задаваемого формой слева, в весовом пространстве Соболева с нормой, задаваемой интегралом справа.

Причем тут нормы в пространствах Соболева (они так не определяются).
Нормировка $f(1)=0$ несколько мешает делать почти постоянной функцию (если не ноль, то тривиально).
Но можно взять функции типа $f(x)=(1-x^{\alpha})^l$ при малых $\alpha$ функция становится почти постоянной.