Мое решение задачи.
Дано: выпуклый четырехугольник, являющийся сечением пирамиды с квадратным основанием; сторона квадрата равна

; через вершину и неизвестную точку

, лежащую на основании пирамиды, проведена прямая, пересекающая выпуклый многоугольник в точке

.
Найти: найти расстояние от точки

до сторон квадрата.
Решение.
Привожу решение для четырехугольника, у которого все стороны не параллельны (для квадрата и трапеции построение проще, но требует пару оговорок). Все построения на плоскости и не требуют выхода в 3D.
1. Обозначим выпуклый четырехугольник

так, что

- острый угол (если нет ни одного острого угла, то

квадрат).
2. Продолжим стороны четырехугольника

до пересечения в точках

.
3. Проведем через

прямую, параллельную

. Точки пересечения этой прямой с продолжением сторон четырехугольника

обозначим

, так что

.
4. Строим окружность с центром в

и радиусом

.
5. Опустим перпендикуляр к прямой

из

до пересечения с окружностью в точке

.
6. Соединим отрезком точки

.
7. Перпендикуляры к отрезку

, проведенные через точки

; прямая, проведенная через точку

и параллельная отрезку

; и сам отрезок

образуют квадрат

.
8. Прямые

пересекаются в точке

.
9. В четырехугольнике

через точки

проведем прямую, пересекающую одну из граней

в точке

. Через эту точку

и точку

построим прямую, которая пересечет одну из граней

в некой точке

.
10. Точка

находится на пересечении

и
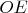
.
11. Все квадраты подобны, поэтому зная отношение расстояний от точки

до граней квадрата

, можно через длину стороны квадрата в основании пирамиды найти расстояние от точки

до сторон квадрата в основании пирамиды.

и FG за фокальную "плоскость"
Если бы еще знать, что это.



