если для простого числа

и натуральных чисел
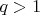
,

,

имеет место равенство

то

--- простое число.
Да, здесь другие идеи, но рассуждения в целом стандартны.
Интересно, каковы они здесь? Неужели это реально решить простыми соображениями?!
(неправильное решение)
Это избыточно сложное и ошибочное решение.
Я устал решать

, поэтому воспользуюсь танчиками:


. Для использования

необходимо

, потому случай

сначала разберем отдельно:
1) Пусть

. Получаем

,

нечетное. Если

, то

, значит

, значит

. В правой скобке число слагаемых нечетно (в силу

), значит

значит

, а

, что невозможно при

. Значит

, значит

- простые Мерсенна, их показатель прост.
2) Пусть

. Тогда

, значит

. А теперь танчик.: Для любых

существуют

:

, где

- результант. Сам результант круговых многочленов известен (см. Прасолова Многочлены):

(здесь в формуле

- произвольное простое, никакого отношения к исходному уравнению не имеющее. Дальше оно не используется, а используется

из уравнения).
Поскольку

, то

. Теперь, если

имеет хотя бы

различных простых делителя, то их результант равен

, получаем противоречие

. Значит

. Тогда уравнение принимает вид

. Каждый множитель слева является степенью

. Кроме того,

, а поскольку

- возрастающая функция, то

, а значит все множители являются различными степенями простого

:

. Если

, то в произведении слева присутствует член

. Разность

в силу

. Отсюда наконец получаем

, т.е.

, что явно невозможно. (Здесь как раз ошибка:

- это не степень простого, значит не факт, что именно

делится на

)
Т.обр,

не может имет различные простые делители, а если

, то

невозможно, значит

- простое.



