Я всё-таки ещё раз поясню ошибку для тех, кто, может быть, будет читать эту тему потом. Но я буду использовать свои обозначения, поскольку они, в отличие от обозначений
rvsn, однозначно понимаемые. И буду использовать свой рисунок.
Выпишу также преобразования Лоренца. Координаты в ИСО детектора

обозначаются

и

с индексом, указывающим на точку, для которой берутся координаты; аналогично координаты в системе отсчёта источника

обозначаются

и

с соответствующим индексом. "Неподвижная ИСО" -

, "движущаяся ИСО" -

.

Как построить оси

и

на этом рисунке? Ось

системе

имеет уравнение

, ось

- уравнение

; подставляя это во вторую пару формул, получим в системе

уравнения

и

соответственно.
Пусть источник света находится в начале координат движущейся ИСО, а фотодетектор расположен в точке

неподвижной СК. В момент времени, когда начала координат совпадают

и

, источник излучает короткий импульс света в сторону детектора.
Мировая линия сигнала изображена красным цветом.
Время детектирования в ИСО, в которой детектор неподвижен, равно

.
В моих обозначениях

,

.
За время

источник света переместится на расстояние

.
В моих обозначениях

,

.
В соответствии с преобразованиями Лоренца часы в месте расположения источника в момент детектирования покажут время

.
Э-э-э... Вот это место уже опасное. "Момент детектирования" в какой системе отсчёта? Написанное Вами выражение соответствует точке

, то есть,

. Это можно проверить: в прямоугольном (по Минковскому) треугольнике с гипотенузой

вертикальный катет равен

, горизонтальный -

, тогда длина гипотенузы

(то есть, интервал между точками

и

) равна

, а показания часов ИСО

в точке

-

. Таким образом, речь идёт о моменте детектирования в системе детектора.
Это означает, что по этим часам промежуток времени от момента излучения

до момента детектирования равен

.
А вот это неправда. На пространственно-временной диаграмме линии одновременности в системе

параллельны оси

. Видно, что в ИСО

точки (события)

и

не одновременны. Одновременными являются

и

. Поэтому

.
С другой стороны, координаты отклика фотодетектора в движущейся ИСО можно рассчитать непосредственно при помощи преобразований Лоренца без использования уравнения движения импульса света в штрихованной системе координат. Подставляя в формулы Лоренца координаты детектирования

, получим их значения в движущейся ИСО

;

Ну, если исправить опечатку, то будет правильный результат:

.
В первой части ответа получен результат, совпадающий с выражением (1) моего вопроса, но, как я понял, он соответствует точке зрения неподвижной ИСО. Второй же результат, который совпадает с выражением (2), соответствует точке зрения движущейся ИСО. Предположим, что такой эксперимент готовится заранее двумя наблюдателями разных ИСО, и они решают задачу, где надо расположить наблюдателя в движущейся ИСО, чтобы он смог наблюдать момент детектирования детектором неподвижной ИСО. Первый (неподвижный), что надо будет расположиться в точке, соответствующей выражению (1), а второй (движущийся) с ним не согласится, так как считает, что надо располагаться в соответствии с выражением (2). По-прежнему не ясно: кто же прав?
Это нечто феерическое. Никому не надо "располагаться в соответствии с выражением". Каждый располагается там, где считает удобным, и рассчитывает момент детектирования в соответствии со своими наблюдениями. Наблюдателю нужно засечь по своим часам момент прихода сигнала о детектировании импульса и вычесть из показаний часов время распространения сигнала от детектора до наблюдателя. Советую проделать это упражнение.
Поясню на постореннем примере что меня «напрягает». Предположим, что мне надо вычислить длину гипотенузы, если известны оба катета. Это можно сделать либо по теореме Пифагора, либо по формуле площади треугольника, выраженную через его стороны, либо по тригонометрическим формулам и т.д. Однако результат всегда будет один, что свидетельствует о самосогласованности и полноте евклидовой геометрии в пределах её постулатов.
Совершенно верно. Если не делать ошибок, то результат будет одинаковым при любом способе вычисления гипотенузы. В СТО - то же самое. Если вычислять некоторую величину разными способами и не делать при этом ошибок, то результат будет получаться одинаковым. СТО в той части, которая здесь обсуждается - это геометрия Минковского. Такая же самосогласованная, как и геометрия Евклида. В чём именно состоит Ваша ошибка, Вам объяснили четыре раза до меня, а здесь Вы читаете уже пятое объяснение.
сначала определяются координаты источника в неподвижной ИСО. Т.к. в неподвижной ИСО события «источник света находится в точке

и «детектор сработал» одновременны, то часы в точке

неподвижной ИСО показывают время

.
Возражений в этом месте нет.
Затем определяется какое время показывают часы в месте расположения источника в движущейся ИСО (в этом месте используется «диаграммный» метод), получается

(*).
На диаграмме видно, что этот момент соответствует точке

. Но это не есть момент детектирования сигнала по часам системы

. Это более поздний момент.
Т.к.

имеет смысл времени исчезновения импульса света, то и (*) несёт такую же нагрузку, но по часам источника
В этом месте и прячется ошибка: Вы подменяете точку

точкой

.
Кстати, а зачем Вам два происшествия в точке

(детектирование сигнала и исчезновение сигнала)? Почему нельзя обойтись одним? Они же имеют одинаковые координаты в любой системе отсчёта. Чтобы успешней себя запутать?
Скажите, пожалуйста, когда часы в неподвижной ИСО в точке

показывают время

, какое время показывают часы в движущейся ИСО? Я его неправильно определил?
Правильно. Только оно не имеет отношения к моменту детектирования сигнала в движущейся ИСО'.
В этом методе ничего не говорится об одновременности или не одновременности событий, так как эти понятия в систему постулатов СТО не входят
Зато эти понятия входят в определение системы отсчёта, и невозможно определить координаты события, не учитывая определение одновременности. Кстати, соотношения, которые Вы используете (преобразования Лоренца,

и тому подобное), выводятся именно из стандартного в СТО определения одновременности; при желании можно использовать другое определение одновременности, не эквивалентное определению Эйнштейна, тогда все формулы станут другими - более сложными.
При наличии сокращения Лоренца координата детектора в движущейся ИСО равна

(‘).
Да, это просто преобразование Лоренца.
Уравнение движения детектора в движущейся ИСО имеет вид

. При этом

.
Уравнение движения правильное, но вот

подкачало. В момент времени

детектор находится в точке

. В прямоугольном треугольнике с гипотенузой
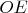
горизонтальный катет имеет длину

, точке

соответствует момент времени

(посмотрите уравнение оси

в начале сообщения), поэтому вертикальный катет равен

; поэтому расстояние

до детектора в момент

равно длине гипотенузы
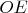
, то есть, по правилам геометрии Минковского,

.
Здесь тоже допущена ошибка? Какая?
Ну, ошибку я указал. Продолжите теперь свои вычисления и посмотрите, что получится.