Уважаемые знатоки,предлагаю вашему вниманию простое решение задачи.
Если у косоугольного треугольника стороны, высота и отрезки, на которые высота делит
сторону, на которую она опущена, имеют целочисленное значение, то решение выглядит
следующим образом. Задаемся значением высоты

, где
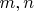
- нечетные числа.
Определяем значения сторон прямоугольных треугольников, из которых состоит
косоугольный треугольник.
Гипотенуза первого прямоугольного треугольника ( сторона косоугольного треугольника) равна:

Гипотенуза второго прямоугольного треугольника ( сторона косоугольного треугольника) равна:

Катет первого прямоугольного треугольника ( часть третьей стороны косоугольного треугольника) равен:

Катет второго прямоугольного треугольника ( часть третьей стороны косоугольного треугольника) равен:

Сложив катеты

и произведя соответствующие преобразования, получим длину третьей стороны:

Отсюда следует, что:

Высота не равна стороне, на которую она опущена.
Площадь треугольника равна:

Площадь косоугольного треугольника не равна квадрату числа. Если бы она равнялась квадрату числа,
она должна быть равна

,
при этом сторона

должна быть равна:

.
Для высоты

доказательство аналогичное.
С Рождеством Христовым всех добрых людей!