Разработанная Эйнштейном специальная теория относительности (СТО) устанавливала равноправие всех равномерно движущихся относительно друг друга инерциальных систем отсчета (СО) прямоугольных координат, связанных лоренцевым преобразованием при переходе из одной СО в другую. Такая ситуация позволила рассматривать все ИСО как различные координатные системы в едином 4-мерном пространственно-временном континууме, а также отказаться от рассмотрения эфира, заполняющего, как ранее предполагалось, абсолютное пространство. (Далее в некоторых случаях термин эфир заменяется термином (риманово) пространство.)
После создания общей теории относительности (ОТО) Эйнштейн осознал важную роль в физических процессах ранее отрицаемого им эфира. Тем не менее эфир не нашел отражения в его ОТО. Автор темы попытался восполнить этот пробел, вводя в ОТО волновые уравнения, определяющие движение эфира, а также других объектов (светового пучка и тел конечной массы) относительно СО координат и эфира. Автором был предложено новое модифицированное решение задачи Шварцшильда для центрально-симметричного вакуумного поля тяготения, исследованное с помощью волновых уравнений.
При разработке ОТО Эйнштейном прежде всего производилось обобщение СТО на произвольные координатные системы при сохранении 4-континуума, относящегося теперь к классу плоских псевдоримановых пространств. Далее рассматривались искривленные псевдоримановы пространства, и устанавливалась связь между тензором энергии импульса и риччиевой кривизной пространства. При этом на допустимые значения метрического тензора и преобразования пространственно-временных координат накладывался ряд ограничений, которые указаны в источнике [1] (пар. 84). Однако, что касается решения проблем ОТО, то в этом случае, по мнению автора, не требуется обязательного выполнения всех указанных ограничений, касающихся метрического тензора. Здесь - основная задача - определение оптимальной СО и вместе с тем волновых уравнений, корректно описывающих материальные поля и объекты.
При этом в первую очередь представляет интерес светоскоростное (световое) уравнение, которое позволяет исследовать свойства поля тяготения и эфира. Указанное волновое уравнение записывается согласно представлению оператора Даламбера в римановом пространстве в следующем
общем виде:

(1)
Здесь

.
Решая это уравнение, можно определить скорость движения эфира и его деформацию во времени. При этом координатная скорость эфира определяется как среднее значение координатных скоростей прямой и обратной световой волны, а деформация эфира - путем анализа изменения скорости эфира в пространстве и времени. Волновое уравнение, получаемое добавлением к левой части светового уравнения (1) члена

(это скалярное уравнение Клейна-Гордона-Фока для

в произвольных координатах), может использоваться для определения скорости и траектории движения свободного тела в гравитационном поле.
Решение полученных волновых уравнений удобно производить спектральным методом, при этом волновые уравнения принимают алгебраическую форму

. На основании последнего уравнения по формуле для групповой скорости сигнала

можно вычислить координатные скорости светового сигнала или тела с конечной массой, которые дают информацию о скорости движения и деформации эфира, а также о скорости и траектории контрольного объекта.
Примером не вполне корректного представления в ОТО, где новая методика позволяет уточнить вопрос, является известное решение Шварцшильда (РШ). Во-первых, РШ непригодно для описания центрально-симметричного гравитационного поля вблизи сильно локализованного тяготеющего тела (внутри сферы Шварцшильда). Во-вторых, не вполне поняты некоторые альтернативные решения для центрально-симметричного гравитационного поля (см. например [2], пар. 31.6).
РШ обычно записывается в сферических координатах в виде зависимости квадрата дифференциала интервала от величины радиуса

cферического сечения искривленного пространства

(2)
где

– гравитационный радиус поля,

.
Считается, что метрика (2) описывает стационарный объект, причем переменная

может принимать значения от нуля до бесконечности. Поскольку характер решения резко изменяется при смене знака разности

, принято вести речь о внешнем

и внутреннем

РШ, описывающих единый объект. При этом в отличие от внешнего внутреннее решение Шварцшильда считается не до конца понятым. Проблемы с пониманием метрической структуры внутреннего РШ связаны с использованием шварцшильдовой системы координат вида 4-континуума, в которой нарушается требование сохранения положительного значения метрического коэффициента

и отрицательного значения коэффициента
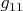
.
Вопреки принятому мнению, согласно канонам ОТО внешнее и внутреннее РШ описывают два резко различающихся объекта, причем в отличие от внешнего внутреннее решение описывает нестационарный объект. Действительно, при

метрический коэффициент
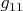
, отвечающий координате

, становится положительным, а коэффициент

при координате

– отрицательным, и таким образом вопреки первоначальному соглашению переменная

здесь играет роль временной координаты, а переменная

– роль радиальной координаты.
Временная координата здесь совпадает с радиусом сферического сечения объекта, который не зависит от радиальной координаты

. Из вышесказанного следует, что рассматриваемый объект представляет собой своеобразный туннель со сферическим сечением, постоянным вдоль его длины и изменяющимся во времени. Отметим также, что рассмотренное нестационарное вакуумное внутреннее РШ описывает самостоятельный изолированный от вселенной континуальный объект, и представляет собой формальное математическое образование, которое, по-видимому, не имеет никакого отношения к реальной действительности.
Если же попытаться рассматривать во внутреннем РШ переменные

и

, как временную и, соответственно, радиальную переменные, придется иметь дело с их мнимыми значениями.
Преобразованием пространственно-временных координат на основе решения Шварцшильда могут быть получены другие альтернативные метрические формы, отвечающие центральному полю тяготения. В частности, определенный интерес представляет метрическая форма Леметра (см. [1] пар.102), которая отвечает всем указываемым в ОТО ограничениям, и таким образом, отображает метрику некоторого искривленного 4-континуума. Однако решение Леметра, описывая нестационарное поле, характеризующееся расширяющейся со скоростью света центральной сферой с неопределенной внутренней метрикой, совершенно не отражает реальную физическую картину центрального поля тяготения.
В свете не удовлетворительного описания центрального поля тяготения с точечной сингулярностью известными метриками большой интерес представляет описываемые ниже варианты метрики, получаемые на основе метрики Шварцшильда путем преобразования временной переменной по формуле

. (3)
Новым координатам соответствуют следующие метрические коэффициенты:


(4)
Здесь последовательность знаков дублета в выражении

отвечает знакам дублета

в формуле (3).
Новые решения характеризуются прежним темпом времени для каждого значения

, однако для каждого значения

, как следует из преобразования (3), добавляется некоторое временное смещение, резко возрастающее вблизи сферы Шварцшильда.
Отметим, что ввиду разрывного характера преобразования (3) мы получаем принципиально новые решения, удовлетворяющее базовым уравнениям ОТО. Все компоненты тензора Риччи здесь равны нулю, при этом на сфере

уже не наблюдается никакой особенности.
Казалось бы, что рассматриваемые решения ввиду непостоянства знака коэффициента

не удовлетворяет требованию представления переменных

в качестве коэффициентов метрического тензора непрерывного 4-континуума, однако наличие отличных от нуля членов

и

существенно меняет дело.
Сосредоточим далее внимание на отвечающих указанным коэффициентам световых волновых уравнениях, которые в случае радиально-симметричной быстро изменяющейся волновой функции имеют вид

. (6)
Анализируя метрики (4), можно понять, что они описывают плоское 3-пространство неинерциального типа. А именно, рассматриваемые метрики отвечают центронаправленному и обратному движению эфира с переменной скоростью

, отвечающей по модулю классической скорости падения свободного тела из бесконечности на тяготеющий объект.
Для доказательства справедливости нашего замечания выполним анализ волнового уравнения (6) согласно методике, описанной в начале статьи. Вычисляя групповую скорость движения светового пучка, получаем следующие выражения для первого и, соответственно, второго знака дублета в выражениях (3,4)

и

. (8)
Здесь знаки нового дублета отвечают направлению движения контрольного светового луча - от центра и к центру СО.
Очевидно, что первому выражению отвечает эфир, устремляющийся к центру координат

, а второму - эфир, разлетающийся от центра с прежней зависимостью скорости от радиуса

. Отметим, что при

радиальная скорость эфира превышает скорость света, что объясняет невозможность выхода светового луча из-под шварцшильдовой сферы в случае центронаправленного движения эфира.
Интегрированием выражений для радиальной скорости эфира можно получить зависимость времени его перемещения между начальным и конечным значениями радиуса. Анализ приведенных формул для скорости падающего из бесконечности тела или светового луча, движущихся к центру тяготения, в варианте СО с центронаправленным движением эфира показывает конечность интервала времени, затрачиваемого на падение от некоторого начального радиуса до центра координат. Например, время падения тела от радиуса

на сферу Шварцшильда примерно равно

, а время падения с той же точки на центр координат -

. В случае решения с разлетающимся эфиром падение на центр координат невозможно, а время падения на сферу Шварцшильда равно бесконечности. Однако собственное время падения от

на сферу Шварцшильда во всех случаях одинаково, и примерно равно

.
Возвращаясь к РШ, укажем формулу для значения прямой и обратной радиальной скорости света,

(9)
получаемую из волнового уравнения для внешнего РШ

Можно видеть, что в этом случае численное значение скорости не зависит от направления светового луча (эфир неподвижен), и стремится к нулю при приближении к поверхности Шварцшильда.
Казалось бы, что ввиду указанного выше различия, касающегося движения объектов вблизи и внутри сферы Шварцшильда, две из трех рассмотренных метрических систем должны быть отброшены, как неверные. Но на самом деле все системы приемлемы, каждая в своем конкретном случае. Так, если масса тяготеющего тела относительно невелика, и мы не имеем дело с реальной сферой Шварцшильда вне тяготеющего тела, удобно использование метрики внешнего РШ, которая отвечает статическому состоянию эфира. При теоретических же исследованиях разумно использовать метрики (4), которые не имеют особенностей на сфере Шварцшильда и допускают непрерывное изменение переменной

от нуля до бесконечности. Метрики (4) удобны при исследовании явления коллапса и "черных дыр".
Может показаться, что решение, отвечающее разлетающемуся пространству, не может иметь никакого отношения к реальной действительности. Но это не так. Математический анализ скорости движения эфира показывает, что, несмотря на периферийное движение, ускорения эфира и свободного тела в каждой точке пространства, отвечающей некоторому значению радиуса, имеют те же значения знака и количественной величины, что и в случае центронаправленного движения эфира.
При использовании метрики (4) определенный интерес представляет зависимость потока эфира через центральное сферическое сечение от его радиуса

, которое описывается выражением

.
Из формулы следует, что рассматриваемый поток падает до нуля при приближении к центру координат. Эфир как бы поглощается при движении к центру и рождается при движении от центра в одинаковых количествах. Такая особенность поведения эфира наводит на мысль относительно единства обеих решений (4). А именно, представляется уместной гипотеза, что мы имеем дело с двумя параллельными вселенными, связанными переходом эфира из одной в другую с максимальной интенсивностью этого перехода в зоне одной или множестве сингулярных точек. При этом одна из рассматриваемых вселенных расширяется, а другая - альтернативная сжимается при сохранении суммарного объема эфира.
Возникает важный вопрос: в какой вселенной существует наш мир - расширяющейся или сжимающейся?
Касательно этого вопроса можно сделать некоторые предположения. Вероятно, мы живем в расширяющейся вселенной, о чем свидетельствует эффект Хаббла. При этом расчетное значение постоянной Хаббла, исходя из средней массы и плотности распределения галактик, принимаемых за сингулярные центры рождения эфира, примерно совпадает с расчетным значением, получаемым из формул для расширяющейся вселенной, найденных А.А.Фридманом.
Для более подробного ознакомления с вопросом см. статью "Волновые уравнения в ОТО и центрально симметричное поле тяготения"
http://www.sciteclibrary.ru/rus/catalog/pages/11123.html ПЕРЕЧЕНЬ ЛИТЕРАТУРЫ
1. Ландау Л.Д., Лифшиц Е.М. Теория поля. Том 2, Москва, ФИЗМАТЛИТ, 2003.
2. Ч.Мизнер, К.Торн, Дж.Уилер. Гравитация. Т3. М. Мир, 1977



