Хм, вообще говоря, это вопрос ... Можно ли неким выбором констант

в такой системе заставить переменные

стать отрицательными. В каждом уравнении в правой части стоит 1, что гарантирует положительность этой правой части на некотором интервале. А следовательно и соответствующая компонента будет положительной (производная больше 0). И так для каждой компоненты (хотя величина этого интервала может и уменьшаться с ростом номера). Все это выглядит слишком фантастичным, но кто знает ...
С другой стороны, при определенных условиях легко оценить вклад, скажем,

в

. Пусть на некотором интервале
![$[0,T]$ $[0,T]$](https://dxdy-03.korotkov.co.uk/f/a/a/b/aab0f08201b211261f795050337fa8df82.png)
справедливо неравенство

. Тогда на этом интервале

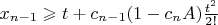


Ясно, что в конце концов для

получится точно такой же ряд как и выше, но с некой добавкой вида

При условиях

эта добавка стремится к 0 с ростом номера

(при

).
Фактически мы получили точное решение в виде ряда.
Аналогичные оценки справедливы и для других компонент (уравнения в сущности инвариантны относительно сдвига номеров).
Отсюда следует справедливость неравенств для решений ограниченных в

.
(Оффтоп)
Можно, конечно, и дальше повозиться с этими неравенствами, но какой смысл?
-- Пт дек 14, 2012 16:54:06 --С другой стороны величина

сама зависит от

и может расти. Короче нужна уже более точная постановка задачи. В том числе и класс допустимых решений. А так это все как-то неопределенно получается.



