У нас там получится два неравенства для скорости. Там есть два минимума: один для ближнего, другой - для дальнего.
Это правильно. А дальше - неправильно. Если бы вы построили графики этих функций при разных исходных данных, вы бы увидели все возможные варианты.
У нас 2 графика 2-х функций, вторая производная всегда положительна - выпуклость вниз, с разной областью определения - минимальный угол для дальней точки меньше чем для ближней - вертикальные асимптоты являются значениями углов "прямой видимости" вершин из точки вылета. Правая вертикальная асимптота общая и равна
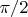
- понятно почему (при приближении к вертикали на нужна большая скорость чтобы перелететь в длину). У этих графиков есть точка пересечения
на общей области определения и минимум у каждого, причем минимум для дальней точки всегда больше. Поэтому мы смотрим - если точка минимума для дальней вершины лежит вне общей области определения - берем точку пересечения, иначе берем точку минимума дальней вершины (через ближнюю получается при этом гарантированный перелет).
Что, впрочем, не мешает вам приложить усилия к нахождению аналитического решения как точки пересечения, так и точки минимума.



