Ааа, я понял!
С одной стороны, ясно, что предел

. С другой стороны, ограничиваясь

, мы можем подобрать такое достаточно большое

, что

для любого
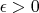
, т.е. исходная функция будет отличаться от

на сколь угодно малый

. А ряд

сходится абсолютно, значит и сумма в нему сходится.
Все

А простые числа вообще не при чем.
Руст,
ex-math, спасибо!
З.Ы.
Ошибка порядка

Может и такая...