Зачем Вам это?
Марков А.А. Элементы математической логики /МГУ(1984) писал(а):
Всякое слово осуществимо путем его писания слева направо, т.е. следующим образом: пишется какая-нибудь буква. К ней приписывается справа другая буква. К полученному объекту приписывается еще буква и т.д. до конца процесса, т.е. до написания последней буквы слова.
Марков А.А. Элементы математической логики /МГУ(1984) писал(а):
При осуществлении слов нам могут встретиться препятствия, такие как край доски, израсходование куска мела, усталость, смерть и т.п. Чем более длинные слова мы захотели бы осуществить, тем больше будут нам мешать подобные препятствия. Правда, их как-то можно обходить: наткнемся на край доски - перенесем дальнейшую часть слова в следующую строку, которую будем мыслить как продолжение только что законченной; мела не хватит - попросим, чтобы принесли из другой аудитории; жизни не хватит - завещаем потомкам, чтобы они закончили слово. Однако ниоткуда не следует, что всегда можно так или иначе преодолеть препятствия, связанные с ограниченностью наших возможностей в пространстве, времени и материале. Наоборот, воззрения современной космологии как-будто свидетельствует об обратном.
Несмотря на это, мы условимся так рассуждать о словах, как если бы при их осуществлении не существовало препятствий, проистекающих от практической ограниченности наших конструктивных возможностей. От этих препятствий мы, таким образом, будем отвлекаться. Эту манеру рассуждать мы будем называть абстракцией потенциальной осуществимости
А я не хочу принимать эту абстракцию. Я не верю, что очень большие числа осуществимы. Я хочу узнать насколько сложную математику можно построить без этой абстракции.
Например, в языке арифметики со знаками умножения и сложения и с инкрементом, обозначаемым штрихом, число 15 можно записать термом

(11 символов). Допустим, что мы согласились принять

. Значит ли это, что мы можем получить число 16, добавив штрих к этому терму справа? Наверное всё же не значит.
У нас пока еще нету знаков умножения, сложения и т.д...
Ну хорошо, замените везде у меня

на

.
Если Вам нужно ввести понятие "осуществимости" натурального числа

, Вы легко можете определить его формулой, выражающей свойство
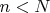
.
Нет, не это я хочу.



