Здравствуйте, участники форума! Буду очень благодарен, если поможете разобраться.
Есть две задачки из сборника упражнений по теории групп Ляпина и др.
1. Определить число и найти все двусторонне стабильные эквивалентности в мультипликативном множестве

, действие в котором задано таблицей:

2.Сколько существует неизоморфных между собою мультипликативных множеств таких, что мультипликативное множество из задачи 1 обладает гомоморфизмом на них?
-----
В 1й задаче я нашел 7 эквивалентностей ( что и с ответом совпадает):
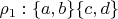






Т.к. фактор-множество

(

) изоморфно своему образу

(эквивалентность

соответсвует гомоморфизму

), то число множеств, искомых в задаче 2 , будет не больше 7. исключаем изоморфные между собой множества ( фактор-множества с одинаковым числом элементов), получаем 4.
В ответе - 5. Неправильно рассуждаю?



