g______d, да, в том и проблема.
Дальнейшие рассуждения.
Пусть есть
(1) :

Существует биекция (как описано выше) между

и

. Следовательно каждой из (1) биективно соответствует
(2) :

Следовательно рассматривая это как ф-цию двух переменных, зафиксируем первую. Тогда каждому

ставиться в соответствие

:

(3) :

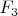
континуально.
Вопрос: как построить биекцию между

и

?
-- 28.10.2012, 20:54 --Есть.
Дана ф-ция

1. Дан

из

. Разобьем

на счетное количество полуинтервалов длины

по обе стороны от нуля. Каждому

поставим в соответствие

, где

- номер интервала в который попал

, а

.
Таким образом (см выше) установлена биекция

. Следовательно по

однозначно установлена

.
2. Фиксируя

в

получаем для каждого

из

множество

.
3. Рассмотрим набор префиксных кодов для всех

:

. По сути каждый элемент

- последовательность натуральных чисел. Закодировав ее в виде

получаем строку

биективно соответствующую элементу в

.
Таким образом:
1.Каждой ф-ции

соответствует ф-ция

. (явное построение смотри выше)
2.Каждой ф-ции

соответствует ф-ция

, где

. (явное построение смотри выше)
3.Каждому элементу

соответствует число из

. (явное построение смотри выше)
Как следствие каждой ф-ции из

биективно поставлена в соответствие ф-ция из

.
Правильно?



