Как правило, берут корень из несмещённой оценки дисперсии (оценка СКО получается при этом смещённой, но величина смещения мала и, во всяком случае, меньше, чем если бы брать корень из смещённой). В принципе избавиться от смещения можно методом "складного ножа", но польза при этом столь мала, а трудности велики, что этим никто не занимается.
Слова "стандартное отклонение" иногда употребляется, как краткий синоним "среднеквадратичного отклонения", но некоторые авторы употребляют его, имея в виду "стандартное отклонение для среднего", которое в
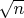
меньше. Поэтому надо внимательно следить за тем, что они имеют в виду.