Хочу предложить гипотезу о том, как строить правдоподобные гипотезы, т. е. такие, которые невозможно(?) опровергнуть.
Гипотеза. Пусть с помощью операций "сложение" и "умножение" задано множество М с качеством

, т.е.

. Для множества М рассматриваем качество

более простое, чем

. Качества заданы с помощью этих же операций. Тогда, если мощность отрицания качества

ограниченная, ненулевая (здесь равная единице(может быть больше единицы?)) и непрерывно отображается

в

или в

, то

непрерывно относительно

или

.
Замечание. Эту гипотезу можно обобщить на большее количество операций. У меня есть идея (очень простая) доказательства этой гипотезы. Настолько простая, что я не уверенна, что такое вообще возможно. Поэтому хотелось бы услышать мнение форумчан по поводу данной гипотезы.
В качестве примеров можно рассмотреть задачи:
1) (Задача из "олимпиадного" раздела). Имеет ли решение в натуральных числах

система (с помощью операций "сложение" и "умножение"):
1)

2)


-

-натуральные числа с качеством


-


-


-разрешимость системы в натуральных числах с помощью заданных операций.


2) Теорема Гурвица (об устойчивости многочленов) не удовлетворяет данной гипотезе. Отсюда её ложность: из-за потери требуемых в гипотезе качеств. Но это отдельная тема. (Теория, строящаяся согласно данной гипотезы, опровергает теорему Гурвица с помощью контрпримера). (Топологическая схема в теореме Гурвица имеет нулевой остаток. А такие источники сигналов (следствие из гипотезы) искривлены).
3) (Задача предложена swec )
1.

2.

С помощью данной гипотезы эта система решается просто при

.

.(отрицательно).
4)


Из гипотезы следует, что это неравенство достаточно доказать в одной точке, например, при

. Но мне эта задача интересна в другом плане, а именно: важность выполнения всех условий, требуемых в гипотезе. Можно проилюстрировать, чем отличается "следование" из непрерывной "правды" от "следования" из непрерывной "лжи". В первом случае мы имеем критерий, а во втором-достаточное условие(в рамках, конечно, условий гипотезы).
5) С помощью данной гипотезы легко вывести новое условие разрешимости уравнений степени
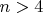
в радикалах, что соответствует их неразрешимости с помощью общей формулы, т.к. существуют уравнения, не обладающие требуемым качеством. Конечно, эта задача меня интересует более всего. Но, прежде стоит разобраться с гипотезой.