Открытые проблемы форумчан.

[ShMaxG]

Вот моя открытая проблема: topic34769.html

Открыт вопрос по существованию особых матриц при $n>4$.

[TR63]

scwec,
ошибку нашла. Она, как я и предполагала, не опровергает моей гипотезы, но ставит, с учётом законов диалектики, новую проблему. Однако сперва надо разобраться с исходной гипотезой. (Ошибка состоит в том, что у Вашей задачи остаток в топологической схеме равен двум, а в гипотезе речь идёт об остатке, равном единице. Отсюда, думаю(предполагаю), нарушение непрерывности процесса).
Забыла сказать ранее, что мне встречались два контрпримера к моей гипотезе: 1) неравенство Харди; 2) гипотеза Пуанкаре. Остаток в их топологической схеме равен нулю, как в теореме Гурвица. Мне бы хотелось простого контрпримерчика, такого, чтобы я была способна уразуметь, где моя ошибка, могла бы в "реале" её пощупать, увидеть воочию, как это сделано мною в теореме Гурвица.
Кстати, если моя гипотеза ошибочна, то в чём тогда причина ошибочности теоремы Гурвица? Мне что-то упоминания о других причинах, вообще, не встречалось.

[Sonic86]

гипотеза о 3 как о примитивном корне
гипотеза о распределении простых чисел

[scwec]

TR63 в сообщении #635492 писал(а):

Мне бы хотелось простого контрпримерчика, такого, чтобы я была способна уразуметь, где моя ошибка, могла бы в "реале" её пощупать, увидеть воочию, как это сделано мною в теореме Гурвица.
Кстати, если моя гипотеза ошибочна, то в чём тогда причина ошибочности теоремы Гурвица? Мне что-то упоминания о других причинах, вообще, не встречалось.

Как Вы будете применять свою гипотезу, например, для системы диофантовых уравнений $x^2+y^2=z^2, x^2+(229y)^2=u^2$.
Имеет она решение или нет? Замените $229$ на $2,4,6,8,10$ и тот же вопрос.

[TR63]

scwec,
хороший пример. Он, хотя не является (с моей точки зрения) контрпримером к моей гипотезе, но намекает, что следует сформулировать в явном виде то, что мной предполагалось в неявном: множество М должно быть полным относительно качества $f_1$.
Если Вашу задачу сформулировать в виде: найти решение системы
1) $x^2+y^2=z^2$
2) $x^2+(ky)^2=u^2$
в натуральных числах, то она не представляет полного множества относительно качества $f_1$, где
$f_1$-это натуральные числа $(x,y,z,u,k)$, являющиеся и не являющиеся решениями системы из двух различных уравнений.
scwec,
если у Вас другое мнение, то прошу изложить его подробнее.

[TR63]

Гипотеза N2. Для разрешимости уравнения пятой степени в радикалах необходимо отсутствие у него качеств, неприсущих уравнениям степени $n<5$. Т. е. достаточно указать хотябы одно качество, присущее уравнению пятой степени и неприсущее уравнениям степени $n<5$, чтобы уравнение пятой степени не было разрешимо в радикалах.
Данная гипотеза является следствием гипотезы N1, сформулированной мною выше. Напомню её:

TR63 в сообщении #631928 писал(а):

Гипотеза. Пусть с помощью операций "сложение" и "умножение" задано множество М с качеством $f_1$ , т.е.$M(f_1)$ (полное относительно этого качества) . Для множества М рассматриваем качество$f_2$ более простое, чем $f_3$ . Качества заданы с помощью этих же операций. Тогда, если мощность отрицания качества$f_2$ равна единице, и непрерывно отображается$M(\bar f)_2$ в$M(f_3)$ или в$M(\bar f)_3$ , то$M(f_2)$ непрерывно относительно$(f_3)$ или$(\bar f)_3$ .

В гипотезе N2 вместо уравнений пятой степени можно рассматривать уравнения теоремы Ферма. Доказательство будет очень простое. В несколько строк. Но основывается оно на первой гипотезе.
Я хочу остановиться на доказательстве теоремы Ферма, т.к. для выяснения условий разрешимости уравнений пятой степени я использую качество, которое применяю для опровержения теоремы Гурвица. Оно простое, но выкладки длиннее. Для выяснения сути действия гипотезы N2 достаточно рассмотреть теорему Ферма. Механизм действия гипотезы в этих задачах одинаков.
$M(f_1)=\{z=\sqrt[n] {x^n+y^n}\}$ (x;y;z;n)-натуральные числа
$f_2=\{корень целой степени (\frac1 n)\}$ корни целой степени
$\bar f_2$-корни не целой степени
$f_3$-неравенство $x+y<(\frac{k+1}{ k})\sqrt[n] {x^n+y^n}$ $k=(1;2)$
$M(f_2)$-уравнения степени $n=1$
$M(\bar f_2)$-уравнения степени $n>1$
Из первой гипотезы следует, что процесс будет непрерывным, т.к. выполнение качества $f_3$ в точках $n=1, n=2$ очевидно. Т. е. все разрешимые уравнения должны обладать этим качеством. Но при $n>2$ это качество нарушается, что и является причиной неразрешимости.
Замечание. Операций здесь две, т.к. возведение в натуральную степень можно считать умножением.
Теорема Ферма легко доказывается в множестве простых чисел (x;y;z) $n=1$, $n=2$. С помощью первой гипотезы результат экстраполируется на все натуральные числа. При $n=3$ теорема легко доказывается с помощью элементарной алгебры, что также подтверждает гипотезу.

[Nilenbert]

TR63 в сообщении #655494 писал(а):

Теорема Ферма легко доказывается в множестве простых чисел (x;y;z) $n=1$, $n=2$. С помощью первой гипотезы результат экстраполируется на все натуральные числа. При $n=3$ теорема легко доказывается с помощью элементарной алгебры, что также подтверждает гипотезу.

Я правильно понял, что вы утверждаете, что теорема Ферма верна при $n=1$ и $n=2$?

[TR63]

Нет.
Под "доказать" я понимаю: подтвердить или опровергнуть. Любую теорему можно рассматривать как гипотезу.Nilenbert,
если Вы хотите понять механизм действия гипотезы или её опровергнуть, то не спешите, читайте внимательно.

[scwec]

(Оффтоп)

TR63, не ответил Вам ранее. К сожалению, у меня нет повода и времени подробно ознакомиться с Вашими, не сомневаюсь, замечательными изысканиями.
Не сомневаюсь, что Вы преданный математике человек.
Наверняка, на форуме найдутся участники, которые захотят разобраться в Ваших выводах.
Извините, но мне совершенно непонятно, что Вы утверждаете. И зачем Вы помянули диофантовы уравнения.
Желаю творческих успехов, не удивлюсь, если Вы член-корр. РАН или хотите им стать. Или что-то в этом духе.

[TR63]

scwec в сообщении #655533 писал(а):

совершенно непонятно, что Вы утверждаете.

scwec, если бы Вы конкретно написали, что Вам не понятно, то я постаралась бы объяснить. Но, поскольку Вас это не интересует, то я пас.

scwec в сообщении #655533 писал(а):

(Оффтоп)

TR63 И зачем Вы помянули диофантовы уравнения.

Я упомянула их в качестве примера. Если Вы читали далее мой ответ, то там всё разъяснено.

(Оффтоп)

Чего я хочу, моё личное дело.

[nikvic]

Задача Словарь для кроссвордов.

Вот задачка, над которой я думал некоторое время. В чистом виде -
Имеем конечный алфавит (не содержащий букву "?") и мноооого слов фиксированной и немаленькой длины.

Требуется выяснить, есть в этом множестве слов слово с данной "маской" - словом той же длины, где некоторые буквы заменены знаком вопроса. Это - индивидуальная задача, а "на практике" такие маски могут поступать как запросы к базе данных. Естественно возникает проблема оптимизации, т.е. построения алгоритма поиска для данного множества с приличной верхней оценкой времени поиска и не слишком "толстого".
Ничего лучше, кроме перебора, не придумал. Спецы по базам данных предложили приёмы, разве что увеличивающие до неприличия размеры алгоритма
====
Первый раз задача возникла, как задача поиска человека по неполным данным.

[_Ivana]

Возможные методы решения зависят от того, какие инструменты у нас есть в наличии и как быстро работает каждый из них. Например, для быстрых отборов в больших массивах по любому набору нескольких полей, я создавал и прописывал дополнительные индексируемые поля, однозначно задающие нужные сочетания этих полей (например, пол+гражданство, пол+гражданство+цвет глаз и т.п.). Это несколько увеличивало размер БД (не критично), но фильтр отбора работал просто моментально.
В случае большого количества возможных сочетаний полей отбора конечно надо искать другие варианты.

[xmaister]

(scwec)

Ну Вы и тролль...

[nikvic]

_Ivana в сообщении #655609 писал(а):

я создавал и прописывал дополнительные индексируемые поля

""""Спецы по базам данных предложили приёмы, разве что увеличивающие до неприличия размеры алгоритма

[TR63]

Замечание к гипотезе N1 и к примеру N3.

Напомню их:

TR63 в сообщении #655494 писал(а):

TR63 в сообщении #631928 писал(а):Гипотеза. Пусть с помощью операций "сложение" и "умножение" задано множество М с качеством , т.е. (полное относительно этого качества) . Для множества М рассматриваем качество более простое, чем . Качества заданы с помощью этих же операций. Тогда, если мощность отрицания качества равна единице, и непрерывно отображается в или в , то непрерывно относительно или

Пример N3

Решить систему:

1. $q^2+p^2=a^2$
2. $q^2+(kq-p)^2=b^2$

$k\ge3, (p,q)=1$

В этом примере я решаю только вопрос о непрерывности процесса, порождаемого топологической схемой относительно переменной k.
Здесь остаток в схеме равен 2, т.е. больше 1. При количественном изменении, согласно диалектике, возможно изменение качества (но, всегда ли?). Т.е., если гипотезаN1 была теоремой, то перестаёт быть теоремой. Имея три экспериментальных примера, можно выяснить условие, при котором вывод, сделанный из гипотезы-теоремы, останется верным. Т. е., порождаемый схемой процесс останется непрерывным. Недостающие два примера есть на форуме "Альтернативная наука" (можно придумать и самостоятельно). Подробности я пропускаю. А вывод таков: пример N3 таким свойством не обладает. Т.е. происходит потеря качества, требуемого для непрерывности процесса. А это означает, что есть смысл искать решение, т.к. становится известно о его существовании. Конечно, это не много, но больше, чем ничего. Чтобы понять, о потере какого качества идёт речь, достаточно записать, чему равно k в примере N3 и посмотреть, чем оно отличается от примеров, приведённых мною на форуме "Альтернативная наука".

Теперь новая гипотеза.

Гипотеза N3.

Максимум количества действительных корней в уравнении степени (n) возможен только при наличии максимума в уравнении производной (это необходимость).

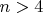
При $1<n\le4$ это легко доказывается классически. А, как при $n>4$. Не знаю. Может, кто подскажет? От этого зависит решение вопроса об обратимости времени. т. е., возможно ли путешествовать в прошлое. По телевизору слышала, что такая возможность следует из ОТО (правда, источник-телевизор не ахти какой; в физике я не разбираюсь вообще). Поверю, если увижу уравнение пятой степени ($x^5+a_2x^3+a_3x^2+a_4x+a_5=0, a_2>0$) с пятью действительными корнями. Т.к. это соответствует интерпритации пространства, в котором мы живём. Саму интерпритацию я приводила в теме "О чём думают грибы" на форуме "Альтернативная наука". Здесь нечто подобное приводил reg81 в теме "Странная задача" 10.02.2012. Эта гипотеза может быть использована для обоснования возможности существования трёхмерной геометрии с необратимым временем.

Гипотеза (новая; информация к размышлению):

Хочу предложить способ вычисления коэффициента искривления пространства-времени. Он заключается в следующем:

1. вычисляем область устойчивости двухосного гироскопического стабилизатора по Гурвицу;
2. вычисляем область устойчивости с помощью моей гипотезы о новой теории устойчивости, которая экспериментально опровергает теорему Гурвица;
3. вычисляем коэффициент искривления путём деления одной величины на другую. Правда (жаль), полученное отношение-не скалярная величина: $k=f(t(a;b;c))>1$. (Не много, но хоть ... )

В образе такой кривизны мне представилась компктификация трёхмерного пространства в одномерное. И, более того: взаимопревращение именно енергии $E=MCC$ и времени T.

(Оффтоп)

Нарочно не придумать.