Когда начинаем говорим о равномерности, то возникает вопрос о равномерности чего? Ведь существует понятие равномерной сходимости последовательности. Поэтому надо пояснить. что разговор в данном случае идет о равномерности средней плотности.
Плотность на каком-либо интервале может быть только средней, так как это частное от деления количества чисел на интервале, удовлетворяющих определенным требованиям, к длине интервала.
О равномерности последовательности, заданной вычислимой функцией

.
Понятие равномерной сходимости последовательности не существует. Можно говорить только о равномерной сходимости семейства последовательностей имеющих дополнительный параметр и равномерная сходимость относится к дополнительному параметру. Все это из другой оперы.
Средняя плотность не имеет параметра локализации и если плотность распределения не всюду одинаковая, как у простых чисел, то она не работает, плохо оценивает количество указанного вида чисел в данном интервале через интеграл. Именно из-за этого появляется необходимость о локализованной плотности, требование к нему как о гладкой в бесконечности функции и оценки погрешности при вычислении через интеграл.
Цитата:
Понятие равномерности средней плотности в теории чисел означает равное количество чисел, удовлетворяющих определенным требованиям, на равных интервалах. например, таким свойством обладают арифметические прогрессии.
Если плотность равномерная, то количество чисел, удовлетворяющих определенным свойством, на любом интервале находится просто - как произведение плотности на длину интервала.
Количество простых чисел на равных интервалах не равны, поэтому простые числа не обладают свойством равномерной средней плотности.
По сути на все это я ответил выше. Понятие равномерности расширяется на случай, когда локализованная плотность не является константой указанным выше способом.
Цитата:
Для нахождения количества чисел, удолетворяющих определенным требованиям, и не обладающим равномерной средней плотности служит определенный интеграл от функции средней плотности по нужному интервалу. в этом случае, произведения средних плотностей на длину интервала суммируются при стремлении длин интервалов к нулю (из определения данного интеграла).
Как уже было сказано, мы не можем устремлять интервалы к нулю при аппроксимации функции натурального аргумента, нам необходимо их устремлять к бесконечности определенным образом. Раз речь идет об интеграле от чего то, то это и есть локализованная плотность. Только ее надо еще более конкретно определить (как выше). При этом появляется автоматический (так как интервалы не устремляются к нулю) погрешность R.
Цитата:
При этом ошибка не возникает, если выполняется свойство асимптотичности. В этом случае справедлива лемма.
Лемма
Пусть

,

и

, то

(6.1) или

(6.2).
Я не понял, к чему это. Обычно плотности стремятся к нулю. То, что отношения интегралов стремятся к 1 так же не говорит о не возникновении ошибок, так как ошибки характеризуются не отношением, а разницей интегралов, которые могут стремится к бесконечности.
Продолжу дальше. Последовательности натуральных чисел, уходящие в бесконечность мы изучаем через распределения при некотором ограничении сверху, устремляя предел ограничения М к бесконечности. Это позволяет изучать распределение таких чисел рассмотрением по большому модулю или множеством более мелких модулей. Изучение по модулю М сводится к распределению чисел

по модулю 1, т.е. распределение дробных частей этой последовательности. Сводя рассмотрение по более мелким модулям, когда распределение по определенным вычетам становится равномерным в смысле постоянной плотности, стоит заново ввести определения для этого случая. По сути это будут прежние определения с функцией плотности 1 для значений в интервале

. При этом локализацию лучше производить не по значениям (тут она постоянная и равно 1), а по n<M. Т.е. если

при оценке на R:

, точка не особая (нормально равномерная).
Все это приводит к родственным с рассмотренными, задачам об распределении количества целых точек в области, при устремлении шага сетки к нулю. Пусть задана область

в плоскости

с дважды непрерывно дифференцируемой границей. Образуем сетку целых точек

и посчитаем количество целых точек при заданных параметрах разбиения на сетку


. Как уже было сказано ранее целые точки на границе считаются с весом
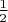
, а угловые даже с весом

. При этом среднее (интегральное по старому) значение количества целых точек определяется через площадь S -

, соответственно погрешность

Изучение погрешности при устремлении к нулю шагов разбиения приводит к оценке

сумм типа

по аналогии с тригонометрическими суммами, которых я называю

суммами:

Здесь

На самом деле

суммы в чем то более удобны, чем

суммы и их оценки сверху обычно отличаются только на константный множитель. Об этом в дальнейшем.



