Вы правы на 50%.

и зависит и не зависит от

. Пусть мы свели некую исходную задачу к разностному уравнению первого порядка (в простейшем случае). Решая его, мы тем самым вычисляем траекторию итераций функции

для некоторого (фиксированного) значения y, взятого из заданного полуоткрытого интервала

. Т.е. находим множество значений

и т.д. и обеспечиваем выполнение функционального соотношения только для элементов этой траектории. Смысл сей методы в том. что вдоль траектории константы должны быть неизменны. Вся область определения функции может быть представлена, как объединение траекторий (факторизуется). Для другой траектории, начинающейся в другой точке

, (принадлежащей тому же интервалу), значения констант будут, естественно, другие. И в этом смысле

, или “константа интегрирования” уравнения 2) действительно зависит от

, если переходить от одной траектории к другой, но следует иметь в виду, что в общем случае траектории, соответствующие разным константам (т.е. разным исходным точкам) не пересекаются.
Это соответствует тому, что на полуоткрытом интервале

значение

можно назначать произвольно, приняв (только на этом интервале!)

. Во всей остальной области определения значение

, может быть определено из уравнения).
Т.е. решение функционального уравнения содержащего итерации включает произвольную функцию. Пару месяцев назад я был озадачен этим обстоятельством, в связи с вопросом Хет Зифа насчет

, но потом убедился, что знатокам предмета этот феномен хорошо известен.
P.S.
Тут еще, как нынче говорят, “фишка в том”, что запись решения 1). в форме

, исчерпывает отнюдь не все решения функционального уравнения, а только те, для которых константа
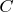
постоянна для всех траекторий. Если все же мы захотим ввести на начальном участке вышеупомянутую произвольную функцию

, то она хитро «растечется» при последующих итерациях, так что аналитическая запись решения станет невозможной, а возможным будет только итерационное задание решения. Только в редких случаях возможно аналитическое задание всех решений, о чем я уже писал в теме ХетЗифа, говоря о пилообразных периодических решениях уравнения

.



