Сведём воедино изложенное введение в теорию групп (с исправлениями).
Группой называется множество

, на котором задана операция умножения, удовлетворяющая трём условиям:
1.

(ассоциативность)
2. существует

, такой что

(существование левой единицы)
3. существует

, такой что

(cуществование левого обратного элемента)
Здесь

,

и

- произвольные элементы

,

и

принадлежат

.
Докажем, что

и

, то есть левая единица является и правой единицей, а левый обратный элемент является и правым обратным элементом.
Действительно, из

следует
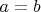
умножением слева на

, поэтому из

следует

.
Далее из

следует

.
Теперь из

следует
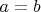
умножением справа на

.
Группа

называется абелевой, если операция умножения коммутативна, то есть

для любых

и

из

.
Множество

, удовлетворяющее только условию 1 (ассоциативности) называется полугруппой.
Вместо операции умножения в определении группы можно говорить об операции сложения.
В этом случае роль единицы играет 0.
Кольцом называется множество

, на котором заданы операции сложения и умножения,
удовлетворяющие следующим условиям:
1.

является абелевой группой по сложению.
2.

является полугруппой по умножению.
3. В

имеют место два дистрибутивных закона:

и

.
Если операция умножения коммутативна, то кольцо называется коммутативным.
В этой теме мы будем рассматривать только коммутативные кольца.
Если существует единица по умножению (которая одновременно правая и левая), то говорят о кольце с единицей.
Полем называется коммутативное кольцо, в котором множество ненулевых элементов является группой по умножению, то есть в котором имеется единица и каждый ненулевой элемент обратим.
Например,

и
![$\mathbb{Z}[\sqrt[n]{2}]$ $\mathbb{Z}[\sqrt[n]{2}]$](https://dxdy-04.korotkov.co.uk/f/f/1/f/f1f1f7257c80036c399f8d26cc2be55082.png)
являются коммутативными кольцами, а

и
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
являются полями.
-------------------------------------------------------------------------------------------
Пусть

- подгруппа группы

.
Тогда

разбивается на подмножества вида

, которые называются левыми смежными классами подгруппы

.
Левые смежные классы либо совпадают, либо не пересекаются.
Если

, то

.
Если же

, то

и

не имеют общих элементов.
Колличество левых смежных классов называется индексом подгруппы

в группе

.
Порядком конечной группы называется колличество её элементов.
Порядок группы

обозначается через
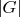
.
Если

подгруппа конечной группы

, то из разбиения

на левые смежные классы следует, что
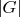
делится на

.
Вместо левых смежных классов можно рассматривать правые смежные классы вида

.
Подгруппа

называется нормальной, если

для любого

, то есть если левые смежные классы совпадают с правыми.
Условие

можно также записать в виде

.
Смежные классы нормальной подгруппы образуют группу по умножению, которая называется фактор группой и обозначается

.
Роль единицы в фактор группе

играет сама подгруппа

.
В абелевой группе любая подгруппа - нормальная.
-------------------------------------------------------------------------------------------
Для того, чтобы непустое подмножество

группы

было подгруппой необходимо и достаточно, чтобы вместе с любыми двумя элементами

и

,

содержало также и

.
Если

- конечное подмножество группы

, достаточно чтобы вместе с любыми двумя элементами

и

,

содержало их произведение
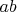
.
Чтобы доказать это, возьмём какой-нибудь

и рассмотрим множество произведений

, где

пробегает все элементы

.
Cреди этих произведений нет равных, поэтому

пробегает все элементы

.
В частности,

при некотором

, откуда

, то есть единица принадлежит

, и из

следует, что

принадлежит

.
Поэтому

- подгруппа.
-------------------------------------------------------------------------------------------
Группа называется циклической, если в ней есть такой элемент

, что все остальные элементы являются его степенями

, где

- целые числа.
Если

- какой-либо элемент группы (не обязательно циклической), то степени

образуют циклическую подгруппу.
Если эта подгруппа конечна, существует минимальное целое положительное число

, такое, что

.
Элементами подгруппы являются:

,

,

, ...,

(в силу минимальности

, среди них нет равных).
Число

называется порядком элемента

.
Таким образом, порядок элемента

равен порядку циклической подгруппы, генерируемой этим элементом.
Группа называется тривиальной, если она состоит из одного единичного элемента.
Тривиальная группа является циклической группой порядка 1.
-------------------------------------------------------------------------------------------
Пусть

- конечная абелева группа, порядок которой делится на простое число

.
Тогда в

cуществует элемент, порядок которого делится на

.
Чтобы доказать это, предположим обратное, и пусть

- такая группа наименьшего порядка, в которой нет такого элемента.
Возьмём какой-либо элемент

, отличный от

, и пусть

- циклическая подгруппа генерируемая этим элементом.
Согласно предположению, порядок

не делится на

, поэтому порядок фактор группы
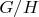
делится на

.
Поскольку порядок этой фактор группы меньше порядка

, то согласно предположению в
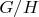
есть элемент

, порядок которого делится на

.
Тогда порядок

делится на

, что противоречит тому, что такого элемента нет.
Пусть

- конечная абелева группа, порядок которой делится на простое число

.
Мы доказали, что в

cуществует элемент, порядок которого делится на

.
Из этого следует, что существует элемент, порядок которого равен

.
В самом деле, если

- порядок элемента

, то порядок элемента

равен

.
--------------------------------------------------------------------------------------------
Пусть

- конечная абелева группа, порядок которой делится на простое число

.
Пусть

- множество всех элементов этой группы, порядок которых является степенью

.
Множество

является подгруппой группы

.
Докажем, что порядок фактор группы
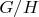
не делится на

.
Предположим обратное, что

делится на

.
Тогда в
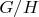
существует элемент

порядка

, где

не принадлежит

.
Поскольку

принадлежит

, то порядок

является степенью

.
Это противоречит тому, что

не принадлежит

.
Таким образом, порядок

равен наибольшей степени

, на которую делится порядок

.
Пусть

- конечная абелева группа, порядок которой делится на простое число

, и

наибольшая степень

, на которую делится этот порядок.
Мы доказали, что существует подгруппа

порядка

.
Поскольку подгруппа

включает все элементы, порядок которых является степенью

, то она является единственной подгруппой порядка

.
--------------------------------------------------------------------------------------------
Абелева группа

называется прямым произведением подгрупп
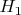
, ...,

, если любой элемент

группы

однозначно представим в виде произведения

, где

, ...,

.
Произведение подгрупп
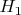
...

является прямым произведением тогда и только тогда, когда выполняется следующее условие:
1) Пусть

, ...,

. Тогда из

следует

,...,

.
Из этого условия следует:
Любые две из этих подгрупп не имеют общих элементов, кроме единицы

.
Все произведения вида

различны.
Пусть

- конечная абелева группа и

, где

, ...,

- различные простые числа.
Пусть
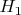
, ...,

-подгруппы порядка

, ...,

.
Мы доказали, что эти подгруппы определены однозначно.
Для них выполняется условие 1).
Произведение этих подгрупп содержит

элементов.
Поэтому

является прямым произведением подгрупп

, и любой элемент

группы

однозначно представим в виде произведения

, где

, ...,

.
-------------------------------------------------------------------------------------------
Элементы

, ...,
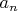
абелевой группы

называются независимыми, если из

следует

, ...,

, для любых целых чисел

, ...,

.
Пусть
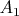
, ...,

- циклические подгруппы, генерируемые элементами

, ...,
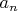
.
Произведение подгрупп

является их прямым произведением тогда и только тогда, когда

, ...,
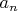
независимы.
Элементы

, ...,
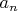
абелевой группы

называются её базисом, если они независимы, отличны от единицы

, и

является произведением циклических подгрупп, генерируемых этими элементами:

.
--------------------------------------------------------------------------------------------
Пусть

- конечная абелева группа порядка

, где

- простое число,

- целое положительное число.
Тогда

представима в виде прямого произведения нетривиальных циклических подгрупп.
Чтобы доказать это предположим обратное, и пусть

-конечная абелева группа наименьшего порядка

, не представимая в виде прямого произведения нетривиальных циклических подгрупп.
Выберем в

элемент

наибольшего порядка, генерирующий циклическую подгруппу

.
Пусть

- какой-либо элемент группы

, не принадлежащий подгруппе

.
Пусть

- порядок смежного класса

в фактор группе

.
Покажем, что можно выбрать такой элемент

, что

.
Если

положим

.
Пусть

,

, где

- целое положительное число.
Пусть

, где
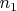
не делится на

, а
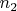
является степенью

.
Тогда порядок

в

равен

, следовательно порядок

в

равен

.
В силу максимальности

имеем:

, откуда

.
Поскольку

и
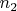
являются степенями

, то
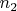
делится на

, значит и

делится на

.
Пусть

.
Тогда

, что и требовалось.
Поскольку

, то циклическая подгруппа группы

, генерированная элементом

не имеет с

общих элементов, кроме

.
В силу минимальности порядка

, фактор группа

является прямым произведением циклических подгрупп, генерируемых элементами

, ...,

, где элементы

, ...,

не принадлежат

и выбраны так, что генерируемые ими циклические подгруппы (группы

) не имеют с

общих элементов, кроме

.
Пусть
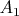
, ...,

- эти циклические подгруппы, генерируемые элементами

, ...,

.
Для любых элементов

, ...,

: если

, то

, ...,

, следовательно

, ...,

принадлежат

, значит равны

.
Поэтому, для любых элементов

, ...,

и любого элемента

: если

, то

, ...,

, значит и

.
Следовательно, группа

является прямым произведением циклических подгрупп
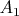
, ...,

и

, что противоречит предположению.
-----------------------------------------------------------------------------------------------------------------------------------
Пусть

- конечная абелева группа порядка

, где

- простое число,

- целое положительное число.
Пусть

является прямым произведением нетривиальных циклических подгрупп
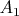
, ...,

.
Подгруппы
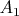
, ...,

не определяются однозначно группой

.
Однако их колличество и порядки определены однозначно с точностью до перестановки.
В частности,

равно числу элементов группы

, имеющих порядок

.
В самом деле, если

, где

, ...,

, то

, ...,

в силу независимости элементов

, ...,

.
Поскольку в каждой из циклических подгрупп имеется ровно

элементов порядка

, то колличество произведений

порядка

равно

.
Пусть теперь

- два разложения группы

в прямое произведение нетривиальных циклических подгрупп, расположенных в порядке убывания их порядков, то есть

и

.
Тогда

|, ...,

.
Для доказательства этого предположим обратное, и пусть

- абелева группа наименьшего порядка

, где

- простое число,

- целое положительное число, для которой это неверно.
Для любой абелевой группы

обозначим

множество элементов вида

, где

.
Множество

является подгруппой группы

.
Если

- циклическая группа порядка

, где

- целое положительное число, то

- циклическая группа порядка

.
Имеем:

- два разложения группы

в прямое произведение циклических подгрупп, расположенных в порядке убывания их порядков.
Среди циклических подгрупп

, ...,

и

, ...,

могут быть тривиальные, но колличество нетривиальных подгрупп одинаково среди

, ...,

и среди

, ...,

.
Обозначим это колличество через

.
Если

, то все подгруппы

, ...,

и

, ...,

- тривиальные, откуда все циклические подгруппы

, ...,

и

, ...,

имеют одинаковый порядок

.
Если

, то это противоречит предположению.
Пусть

.
Поскольку

, то ввиду минимальности порядка группы

имеем:

, ...,

, откуда

, ...,

.
Значит

, ...,

, что противоречит предположению.
(Оффтоп)
Продолжение в следующем сообщении, иначе получается слишком длинное сообщение.



