Господа,
на данные мысли меня навёл парадокс Сколема. Как известно, суть его состоит в том, что если аксиомактика теории множеств изложена на языке логики первого порядка, то теория множеств имеет счётную модель (в которой однако можно определить несчётное множество).
Вроде бы считается, что парадокса "формально" как бы и нет. Сам Сколем, по крайней мере, трактовал его таким образом, что биекция

не существует "в рамках модели" теории множеств, но существует где-то "за рамками её модели". Он даже формулировал это таким образом, что "биекция не является множеством".
Мне такое объяснение показалось весьма странным, ибо доказательство самой теоремы Лёвенхейма-Сколема проведено целиком и полностью в терминах теории множеств (в конце концов, само понятие "язык логики первого порядка" - теоретико-множественное). С другой стороны, сам подход, предполагающий построение т.н. "моделей" теории, показался мне достаточно искусственным. И у меня возникла мысль, а нельзя ли, используя неконструктивную аксиоматику,
напрямую (т.е. без построения "моделей") доказать нечто, противоположное теореме Кантора? Естественно, если бы это было возможно, то, поскольку теорема Кантора тоже доказана, это бы непосредственно свидетельствовало о противоречивости аксиоматики.
Засим предлагаю Вашему вниманию некую схему вывода (сразу предупреждаю, что не безупречную), основанную на предположении о применимости трансфинитной индукции к множеству

, и прошу Вас указать на ошибку.
Сначала, во избежание недоразумений, сформулирую, что я понимаю под трансфинитной индукцией:
Если множество  вполне упорядочено по некоему отношению
вполне упорядочено по некоему отношению  , а
, а  - некое высказывание относительно
- некое высказывание относительно  , то из
, то из  , где
, где  - минимальный элемент
- минимальный элемент  , и из
, и из  выводится
выводится 
В своём выводе я буду пользоваться понятием последовательности неотрицательных действительных чисел, определяемой как:
![$A^{[m]} := \{(k,a_k^{[m]}) : k \in \mathbb{N} \wedge a_k^{[m]} \in [0,+\infty) \wedge \forall i,j : (i = j) \to (a_i^{[m]} = a_j^{[m]})\}$ $A^{[m]} := \{(k,a_k^{[m]}) : k \in \mathbb{N} \wedge a_k^{[m]} \in [0,+\infty) \wedge \forall i,j : (i = j) \to (a_i^{[m]} = a_j^{[m]})\}$](https://dxdy-04.korotkov.co.uk/f/f/d/c/fdcb3a482653402c892fa2688cdc9e6082.png)
Очевидно, что она же - отображение

(не обязательно однозначное). Здесь индекс
![$[m]$ $[m]$](https://dxdy-02.korotkov.co.uk/f/d/d/4/dd493f02a0fe43f96fae4e899577001182.png)
не обязательно подразумевает целое число, а вообще-говоря является
любым ординалом, по смыслу обозначающим "версию" последовательности.
Итак:
1. Возьмём множество

с обычным отношением порядка для действительных чисел. Нетрудно убедиться, что оно вполне упорядочено.
2. Возьмём высказывание
![$P(x) = \exists A^{[m]} \verb $P(x) = \exists A^{[m]} \verb](https://dxdy-02.korotkov.co.uk/f/1/0/1/101c75a779244bbaa54092a8457d187382.png)
(Т.е. "Существует последовательность, содержащая все точки отрезка от 0 до x").
3. Нетрудно убедиться, что минимальным элементом является
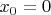
4. Определим нулевую версию последовательности как:
![$A^{[0]} := \{(k,0) : k \in \mathbb{N}\}$ $A^{[0]} := \{(k,0) : k \in \mathbb{N}\}$](https://dxdy-01.korotkov.co.uk/f/4/9/7/497166810287bf828235e28323d7d80f82.png)
(т.е. последовательность из одних нулей). Нетрудно проверить, что она соответствует общему определению
![$A^{[m]}$ $A^{[m]}$](https://dxdy-02.korotkov.co.uk/f/9/5/3/953a4c49d66717ce5206cd794804d33c82.png)
5. Нетрудно убедиться, что
![$\forall t \in [0,0] \verb $\forall t \in [0,0] \verb](https://dxdy-02.korotkov.co.uk/f/d/8/8/d8895336f3453f9414ee549e13dfe65182.png)
, т.е.
![$P(0) = \exists A^{[m]} \verb $P(0) = \exists A^{[m]} \verb](https://dxdy-02.korotkov.co.uk/f/d/5/4/d5479191fbdaafd1c2b45bb1022b542b82.png)
выполнено.
6. Предположим, что

, т.е.

6.1 Возможно, что это самый спорный момент вывода, но поскольку

и поскольку каждому множеству

из данной серии соответствует последовательность
![$A^{[m]}$ $A^{[m]}$](https://dxdy-02.korotkov.co.uk/f/9/5/3/953a4c49d66717ce5206cd794804d33c82.png)
, то должна существовать и последовательность
![$A^{[m]}$ $A^{[m]}$](https://dxdy-02.korotkov.co.uk/f/9/5/3/953a4c49d66717ce5206cd794804d33c82.png)
для множества

, т.е.
![$\exists A^{[m]} \verb $\exists A^{[m]} \verb](https://dxdy-01.korotkov.co.uk/f/4/b/5/4b5925bf7e9cff62e132baaa6d0fb4ef82.png)
6.2 Дополним эту последовательность
![$A^{[m]}$ $A^{[m]}$](https://dxdy-02.korotkov.co.uk/f/9/5/3/953a4c49d66717ce5206cd794804d33c82.png)
числом

следующим образом:
![$a_{k+1}^{[m+1]} := a_k^{[m]} \verb $a_{k+1}^{[m+1]} := a_k^{[m]} \verb](https://dxdy-03.korotkov.co.uk/f/a/9/8/a989a26d224a39f728f0a5e8c35ff4f482.png)
![$a_1^{[m+1]} := x$ $a_1^{[m+1]} := x$](https://dxdy-04.korotkov.co.uk/f/3/5/9/35999e036ac076f19c2f592950543e9382.png)
Таким образом, последовательность
![$A^{[m+1]}$ $A^{[m+1]}$](https://dxdy-04.korotkov.co.uk/f/7/a/7/7a7acc8c3afcc41eb6b3ecf7ebacde6b82.png)
включает все числа
![$\in [0,x]$ $\in [0,x]$](https://dxdy-02.korotkov.co.uk/f/9/7/3/973442bab89e2b5a8b03b351c0399c4082.png)
, т.е. можно утверждать, что:
![$\exists A^{[m]} \verb $\exists A^{[m]} \verb](https://dxdy-04.korotkov.co.uk/f/b/9/8/b98199e4a47cffbb1a5ff397bf886c8682.png)
(здесь изменение индекса версии последовательности не играет роли, поскольку формула утверждает существование
некой версии последовательности)
7. Поскольку предыдущая формула означает

и она была выведена из предположения

, то, применяя трансфинитную индукцию, мы можем записать, что:

Вывод проводился для неотрицательных действительных чисел, однако в него можно включить и отрицательные, выбрав в качестве отношения порядка сравнение модулей, а при равенстве модулей считать меньшим отрицательное число. В таком случае последняя формула записалась бы как:

В переводе на нормальный язык это означает, что точки любого действительного отрезка могут быть пронумерованы. Конечно, я не настаиваю на корректности данного вывода. У меня вызывает подозрение пункт 6.1. Но как-то это всё кажется очень странным, что вопрос состоятельности аксиоматики зависит от таких тонкостей... Может быть существует
прямой способ сделать вывод, противоположный выводу п. 6.1, т.е. что из
 не следует
не следует ![$\exists A^{[m]} \verb $\exists A^{[m]} \verb](https://dxdy-01.korotkov.co.uk/f/8/7/0/8701348462fa5a22f1cb361f148ef35282.png)
?



