Функция

точно не имеет комплексных нулей?
(наврал) их даже найти легко.
Я правильно понял - множество корней бесконечно и все они лежат в

?
Вы правильно поняли
-- Чт май 31, 2012 20:14:20 --А как насчёт
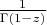
Такая функция не подойдёт, поскольку не является элементарной
-- Чт май 31, 2012 20:20:08 --(Оффтоп)
Нет, есть ещё комплексные корни, например:

Ура! Я избавлен от мучений с интегралом!

Спасибо!
Интересно, недействительные корни это функции в целом как-то закономерно выглядят? Например, действительные - почти арифметическая прогрессия.
Может искомой элементарной функции и нету? Неэлементарную уже нашли...
Думаю, что такая элементарная функция должна существовать



