3.2. (По которой все участники отбора набрали в сумме 0 баллов).
Если рассматривать всевозможные расположения (наборы)

чисел

на окружности, то можно определить операцию суммирования таких наборов как выполнение произведения между парами соответствующих элементов. Заметим, что для любого набора

:

, где

- набор, состоящий из одних единиц.
Если перед каждым шагом Андрей будет поворачивать окружность на одно число против часовой стрелки, чтобы умножать приходилось всегда одну и ту же пару чисел, то преобразование

, производимое над набором, будет всегда одинаковым линейным преобразованием,

. Это преобразование однозначно обратимо,

- обратное к нему преобразование, которое также будет линейным. По индукции легко доказать, что и любая суперпозиция

также будет линейной.
Будем рассматривать всевозможные многочлены с целыми коэффициентами от переменной

и операции над ними, обращая внимание только на чётность коэффициентов получающихся многочленов. Так, к примеру, многочлены

и

будут считаться эквивалентными (далее между ними будем просто писать знак равенства).
Мы можем также формально каждому такому многочлену

поставить в соответствие преобразование наборов

, определённое по формуле

где преобразование

не изменяет набор, как и умножение набора на

, а умножение на

превращает набор в вышеописанный нулевой набор. Можно проверить, что для любого набора
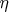
из

чисел

справедливо тождество

где

.
Если

- начальный набор из

чисел
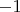
, то условие перехода его в себя после

шагов можно записать как

, где

. Отсюда будет следовать, что

для некоторого многочлена

. Нам нужно доказать, что

Это будет следовать из
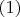
и
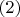
, если рассмотреть многочлен

. С одной стороны, этот многочлен равен

, для некоторого многочлена

, с другой - воспользовавшись тождеством

, справедливым (по модулю

) для любых многочленов

и

и неотрицательного целого числа

, и
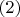
, можно получить, что

. Деля равенство

на

, применяя преобразование

, соответствующее каждой из частей, к

, учитывая
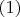
для

и то, что умножение многочленов соответствует суперпозиции соответствующих преобразований

, получим
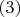
.
Если интересно, то могу написать более подробное решение.



