1. Смысл среднеквадратичного отклонения в том, что это некая мера разброса. Причём для важного частного случая - нормального распределения - наилучшая в смысле эффективная и естественно входящая в выражение для этого распределения (для, скажем, двустороннего распределения Лапласа наилучшее среднее абсолютное отклонение).
2. Нормированным оно не является. Обычно в статистических приложениях под нормированием понимают такое преобразование, которое устраняет зависимость от масштаба. А СКО размерная величина, с той же размерностью, что и у исходной.
3. С его помощью могут быть получены нормированные величины (t-отношение, например, или коэффициент вариации). Интерпретироваться они могут вероятностно (t-отношение) или эмпирически (коэффициент вариации).
4. Не совсем понятно противопоставление стандартного и среднеквадратического отклонения. И, во всяком случае, Википедия тут не авторитетный источник совершенно. Некоторые авторы употребляют эти термины, как синонимические, другие используют их, как различные, чтобы избежать путаницы и сократить выражения (скажем, некоторые авторы говорят о "среднеквадратичном отклонении", имея в виду характеристику случайной величины, и о "стандартном отклонении", имея в виду характеристику разброса среднеарифметического, то есть второе меньше первого в
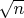
раз.
5. Если у Вас "в среднем полтора мешка плюс-минус пятьдесят мешков", то, значит, у Вас величина, которая принимает как положительные, так и отрицательные значения. Отрицательное число мешков с солью вряд ли физически интерпретируемо. В отличие от "отклонение размера детали от номинала составило в среднем плюс полтора микрона плюс-минус 50 микрон" или "средняя точка попадания отклоняется от центра мишени на полтора метра плюс-минус 50 метров". Если Вы считаете именно мешки с солью (и вообще что-то существенно положительное), то у Вас возможны три случая:
а. Среднее значение велико по сравнению с СКО. отрицательные границы доверительного интервала не случаются, причём число наблюдений достаточно велико, чтобы нормальная аппроксимация работала бы.
б. У Вас малое число наблюдений в выборке, они целые числа, и нормальное приближение слишком грубое. Возможно, стоит перейти к биномиальной или ещё какой учитывающей целочисленность модели. А СКО тут рассчитать можно - но оно не особо осмыслено.
г. Распределение Вашей величины существенно положительно, что не даёт его приблизить нормальным распределением, но есть преобразование (часто это попросту логарифм), приближающее распределение величины к нормальному (например, отношения цен активов "сегодня/вчера" числа положительные, нормальное распределение их приближает плохо, но для их логарифмов уже вполне работает нормальная аппроксимация, и СКО вполне осмыслено, оно, вернее, его нормированная определённым образом величина используется под названием "волатильность".
6. Сравнение стандартных отклонений двух выборок - предмет дисперсионного анализа (как следует из названия, там обычно работают не с СКО, а с его квадратом, то есть дисперсией, но это принципиально не меняет дела). Отношение дисперсий при определённых условиях имеет F-распределение, что позволяет делать выводы о значимости различий разбросов в выборках.
7. Ваша постановка очень похожа на "дисперсионный анализ с повторными измерениями".
-- 01 мар 2012, 10:40 --В смысле постановка "на 10 огурцах намеряли 16 параметров, получили отклонения..."