bayak писал(а):
Параметризованная поверхность данна и

там константа. Если бы я принял её равной единице, то её можно было бы даже и не заметить.

Я предложил понимать Ваши уравнения как выражение старых координат
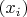
через новые координаты

, чем они, собственно, и являются. Но тогда

, выраженный в новых координатах, должен включать и слагаемое

как одну из компонент. Градиенту ведь нет дела до того, задана ли поверхность

или нет, от этого он не зависит.
Но, раз Вы отказались от трактовки

как координаты, можно

выразить через координаты

, я уже сделал это выше:

. По-прежнему считаю, что Ваши условия

выполнены. Вот градиенты с точностью до скалярных множителей:

Им всем ортогонален

. Более того, они все друг другу ортогональны.
bayak писал(а):
Собственно, в этом случае

, а следовательно имеет место паравращение (парный гиперболический поворот) в плоскостях

и

, т.е.

это функция гиперболического угла.
Такая форма легко интегрируется, получается

. Это не то, что получилось у меня. Но если Вам это подходит -- ОК.




