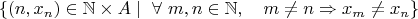Bolzano-Weierstrass (English)

[gefest_md]

Here is a theorem:

Цитата:

Theorem Every bounded sequence of real numbers contains a convergent subsequence.

Here is another:

Цитата:

Theorem Every bounded, infinite set of real numbers has a cluster point.

I found two ways to prove the latter: by contradiction, and directly, by creating some sequence from the set and apply the first theorem. I prefer by contradiction. The direct method I do not understand and some reason follows.
My question is motivated by the second, direct way of proving the theorem about cluster point. Here is the question: Is the following a theorem? "Every bounded, infinite set of real numbers contains a convergent sequence."

Shortly speaking, I want to know how to apply the first theorem in proving the second one.

[Dan B-Yallay]

gefest_md в сообщении #528445 писал(а):

Shortly speaking, I want to know how to apply the first theorem in proving the second one.

If you have an infinite bounded subset of reals, then you can create a sequence. Which is inevitably bounded. Then use the first Theorem.

[gefest_md]

I am pointing out that a prove by contradiction of theorem two convince me more than a proof of it which appeals to theorem one. But I think it is Ok as long as one can fill in the dots in the set $\{(n,x)\in\mathbb{N}\times A\mid\dots\}$.

[Dan B-Yallay]

gefest_md в сообщении #528665 писал(а):

I am pointing out...

Sorry, I did not pay enough attention to the whole post. Only looked for the underlined text.
Anyway, regarding your last comment:

gefest_md в сообщении #528665 писал(а):

But I think it is Ok as long as one can fill in the dots in the set $\{(n,x)\in\mathbb{N}\times A\mid\dots\}$.

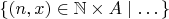
Will have to use the Axiom of Choice (AC)
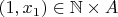
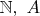
According to AC we can select an element $(1,x_1)\in \mathbb N\times A$ - since both sets $\mathbb N, \ A$ are not empty.
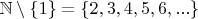
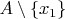
Now, the set $\mathbb N \setminus \{1\} =\{2,3,4,5,6,... \}$ is obviously nonempty, in fact it is still infinite. Similarly, the set $A\setminus \{x_1\}$ is infinite too.
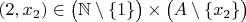
That allows us for using axiom of choice (again), and we can choose $(2,x_2) \in \big(\mathbb N \setminus \{1\}\big) \times\big (A\setminus \{x_2\}\big)$ ... etc.
Thus we get a bounded sequence $\{x_n\}_{n=1}^\infty \subset A$.

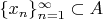
So I guess the set you're looking for has to be written like this:

$$\{(n,x_n)\in\mathbb{N}\times A\mid \ \forall \ m,n \in \mathbb N,\quad m \ne n \Rightarrow x_m \ne x_n\}$$