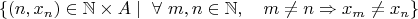I am pointing out...
Sorry, I did not pay enough attention to the whole post. Only looked for the underlined text.
Anyway, regarding your last comment:
But I think it is Ok as long as one can fill in the dots in the set
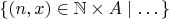
.
Will have to use the Axiom of Choice (AC)
According to AC we can select an element
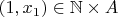
- since both sets
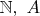
are not empty.
Now, the set
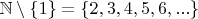
is obviously nonempty, in fact it is still infinite. Similarly, the set
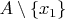
is infinite too.
That allows us for using axiom of choice (again), and we can choose
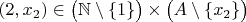
... etc.
Thus we get a bounded sequence
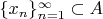
.
So I guess the set you're looking for has to be written like this: