поясните по замедлению времени

[Drac Makac]

(Оффтоп)

хмм..-это нормальный адрес?http://foto.mail.ru/mail/dmitriy1994.94/_myphoto/134.html#

[anatoliy_kiev]

link1519 в сообщении #522542 писал(а):

Пожалуйста помогите разобраться.

Тейлор и Уилер помогут. "Физика пространства-времени" книжка называется. Там этот вопрос подробно разъяснен, нет смысла его переписывать на форуме. Если кратко: никакого противоречия нет (если бы противоречие было, это было бы большим ударом по основаниям СТО). В ситуации, когда мы находимся в системе отсчета наблюдателя A (B пролетает мимо) равенство $t_A = \gamma t_B$ справедливо только тогда, когда события в системе отсчета B происходят в одном месте. Но эти два события не происходят в одном месте в с точки зрения A, поэтому обратный результат $t_B = \gamma t_A$ не справедлив. При этом условия, когда оба события происходят в одном и том же месте в обеих системах отсчета никогда не возникают, если только не $v=0$, но тогда просто $\gamma = 1$ $\implies$ $t_A = t_B$.

Простыми словами, вы пытаетесь сравнивать апельсины с бананами. Вот и получается то, что получается, ведь времена, измеренные наблюдателями в разных системах отсчета -- очень разные вещи. Рассматриваемая ситуация с замедлением времени не более противоречива, чем ситуация, когда два человека разбегаются в противоположных направлениях и при этом оба обнаруживают, что другой человек по мере удаления кажется им все меньшим и меньшим.

[Someone]

(Оффтоп)

Drac Makac в сообщении #522739 писал(а):

это нормальный адрес?http://foto.mail.ru/mail/dmitriy1994.94/_myphoto/134.html#

Это ссылка не на рисунок, а на страницу, где расположен рисунок и ещё куча всякой всячины. Необходима прямая ссылка на рисунок. Получить её можно, щёлкнув правой кнопкой по рисунку и выбрав в выпадающем меню пункт "Копировать ссылку на изображение". В Вашем случае получится ссылка

http://content.foto.mail.ru/mail/dmitriy1994.94/_myphoto/i-134.jpg

[Drac Makac]

воть=

(Оффтоп)

Someone-Спасибо большое!

(Оффтоп)

теперь я могу считаться продвинутым пользователем

[Munin]

(Оффтоп)

Drac Makac в сообщении #522760 писал(а):

теперь я могу считаться продвинутым пользователем

Не раньше, чем научитесь в paint-е буквы писать как текст :-)

[diletant10]

Первая ситуация. С Земли запустили космический аппарат - матку (КА-М). На круговую орбиту вокруг Солнца на расстоянии от Солнца в разы большем, чем максимальное удаление Плутона от Солнца. Плоскость орбиты КА-Ми совпадает с плоскостью орбиты Юпитера. На КА-Ме две одинаковые ракеты. На каждой ракете одинаковые часы, одинаковые источники электромагнитных волн (лазеры) и одинаковые приемники – регистраторы электромагнитных волн. Часы каждую минуту на 30 секунд включают лазеры. Так как, находясь в КА-Ме, ракеты неподвижны относительно друг другу, то приемники каждую минуту 30 секунд фиксируют излучение от лазера другой ракеты без изменения длины волны. И 30 секунд отсутствия излучения.
Вторая ситуация. С КА-Ми одновременно стартуют обе ракеты в противоположных направлениях, перпендикулярных плоскости орбиты КА-Ми. Первая ракета стартовала в направлении на «север». Вторая ракета стартовала в направлении на «юг». Двигатели обеих ракет работали одинаковые интервалы времени по своим часам. Разгон обоих ракет проходил с равными ускорениями по модулю, но с противоположными по вектору. На каждой ракете постоянно за каждую минуту на 30 секунд часы продолжали включать лазеры. При разгоне ракет приемники фиксировали нарастающее удлинение длины волны света и пропорциональное увеличение интервалов излучения лазеров и интервалов отсутствия излучения. После выключения двигателей некоторое время продолжалось фиксирование упомянутых изменений. Из-за конечности скорости света. Затем ситуация с длиной волны света, интервалом излучения лазеров и интервалом отсутствия излучения стабилизировалась. В СО второй ракеты после стабилизации длины волны света от лазера первой ракеты наблюдается следующее. Длина волны света от лазера первой ракеты приемником на второй ракете фиксировалась в n раз длиннее, чем в Первой ситуации. Эффект Доплера. Интервал излучения лазера первой ракеты и интервал отсутствия излучения также увеличились в те же n раз. Увеличение указанных интервалов можно трактовать как замедление времени на первой ракете относительно времени на второй ракете. По СТО вопросов нет. Точно то же и в СО первой ракеты по отношению ко второй ракете. И тоже по СТО вопросов нет.
Продолжение следует...

-- 04.01.2012, 22:17 --

Продолжение предыдущего сообщения.
Третья ситуация. Обе ракеты сменили ориентацию относительно далеких звезд на 180 градусов. И при одних и тех же показаниях своих часов включили двигатели. Модули ускорения как во Второй ситуации. Время работы двигателей в два раза больше, чем во Второй ситуации. Направление движения первой ракеты на «юг». Направление движения второй ракеты на «север». Ракеты летят навстречу друг другу с тем же модулем скорости, с какой они удалялись друг от друга во Второй ситуации. В СО второй ракеты после стабилизации длины волны света от лазера первой ракеты наблюдается следующее. Длина волны света от лазера первой ракеты приемником на второй ракете фиксировалась в n раз короче, чем в Первой ситуации. Эффект Доплера. Интервал излучения лазера первой ракеты и интервал отсутствия излучения также уменьшились в те же n раз. Уменьшение указанных интервалов можно трактовать как ускорение времени на первой ракете относительно времени на второй ракете. Со СТО у меня не сходится. Точно то же и в СО первой ракеты по отношению ко второй ракете. И опять со СТО у меня не сходится.
Четвертая ситуация. Ракеты встретились и продолжили свои полеты, не включая двигателей, удаляясь друг от друга с тем же модулем скорости, с какой они двигались навстречу друг другу в Третьей ситуации и с какой они удалялись друг от друга во Второй ситуации. В СО второй ракеты после стабилизации длины волны света от лазера первой ракеты наблюдается следующее. Длина волны света от лазера первой ракеты приемником на второй ракете фиксировалась в n раз длиннее, чем в Первой ситуации. Эффект Доплера. Интервал излучения лазера первой ракеты и интервал отсутствия излучения также увеличились в те же n раз. Увеличение указанных интервалов можно трактовать как замедление времени на первой ракете относительно времени на второй ракете. По СТО вопросов нет. Точно то же и в СО первой ракеты по отношению ко второй ракете. И тоже по СТО вопросов нет. То есть, все как во Второй ситуации.
Прошу разъяснить Третью ситуацию. Где у меня ошибка?

[Someone]

Ошибка состоит, собственно говоря, в том, что Вы неправильно интерпретируете эффект Доплера как замедление или ускорение времени. "Замедление" времени составляет только часть эффекта Доплера, причём, при сближении - с противоположным знаком. Сейчас не имею времени, но завтра постараюсь расписать подробнее, если кто-нибудь не сделает это раньше.

[Someone]

diletant10 в сообщении #523060 писал(а):

Прошу разъяснить Третью ситуацию. Где у меня ошибка?

Уж больно перегружены деталями Ваши "ситуации". Ошибка состоит, собственно, в том, что Вы неправильно интерпретируете эффект Доплера как замедление или ускорение времени. В релятивистском эффекте Доплера "замедление" времени как таковое составляет только некоторую часть (поперечный эффект Доплера), причём, не всегда с тем же знаком (в том смысле, что поперечный эффект Доплера всегда уменьшает частоту сигнала, в то время как продольный увеличивает или уменьшает в зависимости от направления движения).

Вложение:

CTO-twins-1.gif [ 3.76 Кб | Просмотров: 2279 ]

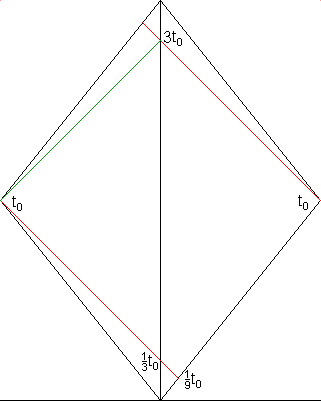
Вот пространственно-временная диаграмма, иллюстрирующая Вашу "третью ситуацию". Ракеты разлетаются в разные стороны, потом возвращаются назад. Этапами ускорения и торможения пренебрегаем, считая их чрезвычайно короткими. Ракеты удаляются от неподвижного наблюдателя со скоростями $v_1=\frac 45c$ в течение $5$ лет по часам неподвижного наблюдателя (относительно друг друга их скорость равна $v_2=\frac{2v_1}{1+\frac{v_1^2}{c^2}}=\frac{40}{41}c$), затем разворачиваются и с такой же скоростью возвращаются назад. Поэтому по неподвижным часам экспедиция займёт $2\cdot 5=10$ лет. Коэффициент замедления времени в ракетах с точки зрения неподвижного наблюдателя составляет $\sqrt{1-\frac{v_1^2}{c^2}}=\frac 35$, поэтому по часам на ракетах этап удаления от точки старта продолжается $t_0=3$ года, и столько же - этап возвращения, то есть, вся экспедиция по часам ракет занимает $2t_0=6$ лет.
Вашу сигнализацию тоже упростим. Пусть каждый из трёх наблюдателей (двое в ракетах и один, оставшийся в точке старта) раз в секунду посылает двум другим короткий импульс, по которому они будут следить за ходом времени у него.

На этапе удаления неподвижный наблюдатель будет видеть приходящие к нему сигналы с частотой $\sqrt{\frac{1-\frac{v_1}c}{1+\frac{v_1}c}}=\sqrt{\frac{1-\frac 45}{1+\frac 45}}=\frac 13$, то есть, один раз в $3$ секунды, поэтому неподвижный наблюдатель будет видеть удаление втрое дольше, то есть, $3t_0=9$ лет. На рисунке зелёная и (верхняя) красная линия изображают мировые линии сигналов, посланных с ракет в момент поворота. Это же время можно посчитать иначе: ракета удаляется (по условию) $5$ лет со скоростью $v_1=\frac 45c$ и оказывается на расстоянии $5v_1=4$ световых года, и сигнал о повороте идёт оттуда ещё $4$ года, всего получается $5+4=9$ лет.
На этапе сближения неподвижный наблюдатель будет принимать сигналы с частотой $\sqrt{\frac{1+\frac{v_1}c}{1-\frac{v_1}c}}=\sqrt{\frac{1+\frac 45}{1-\frac 45}}=3$, поэтому приближающиеся ракеты он будет наблюдать в течение $\frac 13t_0=1$ года. Итого, с его точки зрения, экспедиция займёт $3t_0+\frac 13t_0=\frac{10}3t_0=10$ лет, что согласуется с полученным ранее значением.

Рассмотрим теперь ситуацию с точки зрения наблюдателя, находящегося в ракете (пусть в той, которая на рисунке полетела налево). На рисунке (нижняя) красная линия изображает мировую линию сигналов , которые наблюдатель в левой ракете получает в момент поворота).
Неподвижный наблюдатель удаляется от наблюдателей в ракетах с той же скоростью $v_1=\frac 45c$, поэтому сигналы от него приходят с частотой $\frac 13$, так что в течение своих $t_0=3$ лет наблюдатель в ракете получит от неподвижного сигналы за $\frac 13t_0=1$ год. Затем ракета поворачивает (в этот момент расстояние от ракеты до неподвижного наблюдателя, с точки зрения пассажиров ракеты, составляет $t_0v_1=\frac{12}5$ светового года - коэффициент сокращения расстояния равен $\sqrt{1-\frac{v_1^2}{c^2}}=\frac 35$), и теперь частота приходящих сигналов будет равна $3$, поэтому в течение следующих $t_0=3$ лет наблюдатель в ракете получит от неподвижного сигналы за $3t_0=9$ лет. В итоге наблюдатель в ракете в течение своих $2t_0=6$ лет получит от неподвижного сигналы за $\frac 13t_0+3t_0=\frac{10}3t_0=10$ лет - именно столько, сколько должно быть по предыдущим вычислениям.
Что увидит пассажир ракеты, наблюдая вторую ракету (которая полетела вправо)? В течение первых $t_0=3$ лет (до поворота) наблюдатель будет видеть, что вторая ракета удаляется от него со скоростью $v_2=\frac{40}{41}c$, поэтому частота сигналов, приходящих с другой ракеты, равна $\sqrt{\frac{1-\frac{v_2}c}{1+\frac{v_2}c}}=\sqrt{\frac{1-\frac{40}{41}}{1+\frac{40}{41}}}=\frac 19$. Значит, наш наблюдатель получит от правой ракеты сигналы за $\frac 19t_0=\frac 13$ года (и будет видеть правую ракету на расстоянии $t_0v_2=\frac{120}{41}$ светового года). Затем левая ракета поворачивает, и её пассажир будет видеть правую ракету на постоянном расстоянии от себя и получать от неё сигналы с частотой $1$ в течение $t_0-\frac 19t_0=\frac 89t_0=\frac 83$ года. Когда до финиша останется $t_0-\frac 89t_0=\frac 19t_0=\frac 13$ года, он увидит, что вторая ракета, наконец, повернула и начала приближаться со скоростью $v_2=\frac{40}{41}c$. При этом сигналы от правой ракеты будут приходить с частотой $\sqrt{\frac{1+\frac{v_2}c}{1-\frac{v_2}c}}=\sqrt{\frac{1+\frac{40}{41}}{1-\frac{40}{41}}}=9$, так что за оставшиеся $\frac 19t_0=\frac 13$ года их придёт как раз столько, сколько правой ракетой будет послано за $9\cdot\frac 19t_0=t_0=3$ года. Таким образом, с точки зрения наблюдателя в левой ракете, за его $2t_0=6$ лет в правой ракете пройдёт $\frac 19t_0+\frac 89t_0+t_0=2t_0=6$ лет.

Исправление. По поводу зачёркнутых слов смотрите более позднее сообщение.

[diletant10]

Someone в сообщении #523355 писал(а):

Уж больно перегружены деталями Ваши "ситуации".

В этих деталях все и дело. Уважаемый Someone, или я Вас не понял, или Ваш ответ имеет частичное отношение к моим вопросам. У Вас есть лишь одна «деталь», частота сигналов. Изложу иначе вопросы. Смотрим мое сообщение от 04.01.2012, 22:17. Все вопросы по второй ситуации тогда, когда СО обеих ракет уже есть ИСО (двигатели выключены), и когда свет от каждой ракеты после выключения двигателей (после окончания ускорения) достиг другую ракету. И не рассматриваем СО космического аппарата – матки, доставившего обе ракеты в точку разлета первой и второй ракет. Космический аппарат – матка, выполнив свою задачу, вернулся на Землю, он многоразовый.
Вопрос. Часы обеих ракет синхронизированы?
Вопрос. СО второй ракеты, где вторая ракета неподвижна, является ИСО?
Вопрос. В СО второй ракеты, фиксируемая приемником второй ракеты, длина волны электромагнитного сигнала от лазера первой ракеты в $n$ раз больше, чем длина волны электромагнитного сигнала от лазера на второй ракеты. Длительность сигнала от первой ракеты меньше, чем $30\cdot n$ секунд, но больше 30-ти секунд? Сигнала нет также меньше $30\cdot n$ секунд, но больше 30-ти секунд?
Вопрос. Лазер на второй ракете по своим бортовым часам по-прежнему каждую минуту на 30 секунд включается, и луч от него через некий интервал времени достигает первую ракету. Частично отразившись от зеркала на первой ракете, сигнал достигает вторую ракету. Приемник на второй ракете фиксирует длину волны электромагнитного сигнала от своего лазера, отразившегося от зеркала первой ракеты. Во сколько раз длина волны «вернувшегося» на вторую ракету электромагнитного сигнала больше длины волны излучаемого лазером электромагнитного сигнала, излучаемого лазером этой же второй ракеты? Не в $n^2$ ли раз? Какова длительность сигнала? Меньше, чем $30\cdot{n^2}$, но больше $30\cdot n$ секунд? И каков интервал времени, когда сигнала нет? Меньше, чем $30\cdot{n^2}$, но больше $30\cdot n$ секунд?
То есть, при «разлете» двух ракет с постоянной скоростью (СТО) длина волны электромагнитного сигнала увеличивается в большее число раз, чем длительность сигналов и длительность интервала времени отсутствия их? В этом и заключается наблюдаемое в СО второй ракеты замедление времени в первой ракете, хотя часы в обеих ракетах идут с одной и той же скоростью? А реальное замедление времени относительно ИСО лишь в ускоряющихся СО? Или в области, где напряженность гравитационного поля больше, относительно области, где напряженность гравитационного поля меньше? Так я понял Ваше

Цитата:

В релятивистском эффекте Доплера "замедление" времени как таковое составляет только некоторую часть (поперечный эффект Доплера), причём, не всегда с тем же знаком (в том смысле, что поперечный эффект Доплера всегда уменьшает частоту сигнала.

Я не слишком много напутал?

[link1519]

Спасибо. Кажется разобрался.
Объяснение то очень простое: $t_A = \gamma t_B$ в разных ИСО описывает разные измерительные процедуры.
Но читая про "парадокс" близнецов на synset.com и wikipedia возникли другие вопросы.

На http://synset.com/ru/Парадокс_близнецов написано что объяснить парадокс близнецов можно вообще не прибегая к неИСО.
Цитата :

"Космонавт, летящий мимо любых "неподвижных" часов , видит, что они идут медленнее, чем его собственные. Однако на всех таких часах, встречающихся ему на пути, он наблюдает будущее время. Аналогично, сотрудники космопортов, мимо которых пролетает космонавт, видят его моложе. Пролетающие в это же время мимо брата-домоседа "племянники-одногодки" (на последних кораблях эскадры) выглядят старше землянина. Эти эффекты абсолютны для наблюдателей разных систем, находящихся в одной пространственной точке, поэтому не изменятся при остановке. Для понимания парадокса близнецов, на самом деле, нет необходимости даже рассматривать неинерциальные системы отсчета! Если остановится космонавт, то он "попадёт в будущее" земной системы отсчета и будет там моложе. Точно так же, если ускорится землянин, то он окажется в будущем системы космонавта и там будет моложе.
"
Но ведь это только с точки зрения ИСО космонавта, а сточки зрения ИСО космопорта будет тоже самое (симметрично) ?
В ИСО космопорта должно быть:
"сотрудник космопорта, летящий мимо любых "неподвижных" часов космонавтов , видит, что они идут медленнее, чем его собственные . Однако на всех таких часах, встречающихся ему на пути, он наблюдает будущее время. Ну и соответственно при остановки сотрудник космопорта попадает в будущее космонавта и должен быть моложе.

То есть объяснение парадокса требует рассмотрения этапов не симметричности братьев (ускорения) и без этого никак ?

[Someone]

diletant10 в сообщении #523754 писал(а):

В этих деталях все и дело. Уважаемый Someone, или я Вас не понял, или Ваш ответ имеет частичное отношение к моим вопросам. У Вас есть лишь одна «деталь», частота сигналов.

Вы полагаете, что Ваши детали имеют какое-нибудь значение, и что-нибудь изменится, если интервал между сигналами будет не 1 секунда, а 30 секунд или 30 часов, и результат вычислений станет другим? Или продолжительность сигнала будет не доли секунды, а десятки секунд? Эти сигналы разве как-нибудь влияют на ход времени?
А описание того, как ракеты доставили в точку старта, где она расположена, и что потом стало с доставившим их транспортом, может быть очень увлекательным в фантастическом романе, но совершенно ни к чему в данном случае.

diletant10 в сообщении #523754 писал(а):

И не рассматриваем СО космического аппарата – матки, доставившего обе ракеты в точку разлета первой и второй ракет.

Не надо - не рассматривайте. Просто пропустите в моём тексте то, что относится к неподвижному наблюдателю.

diletant10 в сообщении #523754 писал(а):

Вопрос. Часы обеих ракет синхронизированы?

Движущиеся относительно друг друга часы не могут быть синхронизированы. Процедура синхронизации работоспособна только для часов, которые неподвижны относительно друг друга (и движутся на неизменном расстоянии по инерции).

diletant10 в сообщении #523754 писал(а):

Вопрос. СО второй ракеты, где вторая ракета неподвижна, является ИСО?

Если её двигатели не работают и никакие внешние силы на неё не действуют, то является.

diletant10 в сообщении #523754 писал(а):

Вопрос. В СО второй ракеты, фиксируемая приемником второй ракеты, длина волны электромагнитного сигнала от лазера первой ракеты в $n$ раз больше, чем длина волны электромагнитного сигнала от лазера на второй ракеты. Длительность сигнала от первой ракеты меньше, чем $30\cdot n$ секунд, но больше 30-ти секунд? Сигнала нет также меньше $30\cdot n$ секунд, но больше 30-ти секунд?

Эффект Доплера на все частоты действует одинаково: все частоты увеличиваются (при приближении) или уменьшаются (при удалении) источника сигнала в одинаковое число раз. На все промежутки времени, связанные с сигналом, эффект Доплера также действует одинаково: они все уменьшаются (при приближении) или увеличиваются (при удалении) источника сигнала в то же самое число раз, что и частоты.

diletant10 в сообщении #523754 писал(а):

Вопрос. Лазер на второй ракете по своим бортовым часам по-прежнему каждую минуту на 30 секунд включается, и луч от него через некий интервал времени достигает первую ракету. Частично отразившись от зеркала на первой ракете, сигнал достигает вторую ракету. Приемник на второй ракете фиксирует длину волны электромагнитного сигнала от своего лазера, отразившегося от зеркала первой ракеты. Во сколько раз длина волны «вернувшегося» на вторую ракету электромагнитного сигнала больше длины волны излучаемого лазером электромагнитного сигнала, излучаемого лазером этой же второй ракеты?

Замените зеркало источником сигнала, который излучает точно такой сигнал, какой он принял. И учтите движение первой ракеты в момент ретрансляции сигнала и второй ракеты в момент приёма.

diletant10 в сообщении #523754 писал(а):

То есть, при «разлете» двух ракет с постоянной скоростью (СТО) длина волны электромагнитного сигнала увеличивается в большее число раз, чем длительность сигналов и длительность интервала времени отсутствия их?

Нет, всё увеличивается абсолютно одинаково.

diletant10 в сообщении #523754 писал(а):

В этом и заключается наблюдаемое в СО второй ракеты замедление времени в первой ракете, хотя часы в обеих ракетах идут с одной и той же скоростью?

Нет, не в этом.

diletant10 в сообщении #523754 писал(а):

А реальное замедление времени относительно ИСО лишь в ускоряющихся СО?

Это мне непонятно. Почему Вы так решили?

Есть нестабильные частицы - пионы. Они "живут" очень короткое время, и за время своей жизни, двигаясь со скоростью света, могли бы пролететь (в среднем) $7{,}7$ метра. Фактически пионы высоких энергий пролетают больше $700$ метров, поскольку именно на таком расстоянии стоит мишень для них от того места, где они образуются. Как раз за счёт замедления времени в движущейся ИСО. Как видите, эффект совершенно реальный, хотя об ускорениях речи не идёт.

diletant10 в сообщении #523754 писал(а):

Или в области, где напряженность гравитационного поля больше, относительно области, где напряженность гравитационного поля меньше?

В СТО нет гравитационного поля.

diletant10 в сообщении #523754 писал(а):

Так я понял Ваше

Вы сделали совершенно поразительный вывод их моих слов. Я ничего подобного не говорил. Я говорил только о том, что эффект Доплера - это не замедление времени, хотя некоторая часть его обусловлена замедлением времени.

link1519 в сообщении #523809 писал(а):

... написано что объяснить парадокс близнецов можно вообще не прибегая к неИСО.

Правильно написано.

link1519 в сообщении #523809 писал(а):

То есть объяснение парадокса требует рассмотрения этапов не симметричности братьев (ускорения) и без этого никак ?

Не обязательно рассматривать именно этап ускорения (он может быть очень коротким по сравнению с величиной расхождения времени и не играть существенной роли; можно сформулировать задачу так, что никаких ускорений не будет вообще), но асимметрия обязательно должна быть. Немного выше я рассматривал ситуацию, в которой "близнецы" разлетаются и потом возвращаются симметрично, никакой разницы в прошедшем времени для них не будет.

[diletant10]

Someone в сообщении #523920 писал(а):

А описание того, как ракеты доставили в точку старта, … совершенно ни к чему в данном случае.

Замечание принято. Извините. Но в первом сообщении об этом не писалось и не рассматривалось, однако Вы почему-то начали именно с этого. Поэтому и последовало уточнение.

Цитата:

Просто пропустите в моём тексте то, что относится к неподвижному наблюдателю.

Я в недоумении. Разве в СТО какая-либо ИСО имеет преимущество? Насколько я понимаю в СТО, неподвижным наблюдателем можно считать не только космический аппарат – матку, но и любую из двух ракет. Вы меня запутали.

Цитата:

Движущиеся относительно друг друга часы не могут быть синхронизированы.

Хорошо, принято. Заменим формулировку. Часы на обеих ракетах идут с одинаковой скоростью? (Смотрим Вторую ситуацию в сообщении от 04.01.2012, 22:17).

Цитата:

diletant10 в сообщении #523754 писал(а):

То есть, при «разлете» двух ракет с постоянной скоростью (СТО) длина волны электромагнитного сигнала увеличивается в большее число раз, чем длительность сигналов и длительность интервала времени отсутствия их?

Нет, всё увеличивается абсолютно одинаково.

То бишь, о чем я писал в сообщении от 04.01.2012, 22:17. Но в таком случае, где же замедление времени в первой ракете относительно хода времени в ИСО второй ракеты, в которой вторая ракета неподвижна, а первая ракета удаляется от нее с постоянной скоростью?

Цитата:

Есть нестабильные частицы - пионы. Они "живут" очень короткое время, и за время своей жизни, двигаясь со скоростью света, могли бы пролететь (в среднем) $7{,}7$ метра. Фактически пионы высоких энергий пролетают больше $700$ метров, поскольку именно на таком расстоянии стоит мишень для них от того места, где они образуются. Как раз за счёт замедления времени в движущейся ИСО. Как видите, эффект совершенно реальный, хотя об ускорениях речи не идёт.

Не понял. Разве СО, в которой свободно падающее тело в гравитационном поле планеты неподвижно, является ИСО?

[Someone]

diletant10 в сообщении #524018 писал(а):

Замечание принято. Извините. Но в первом сообщении об этом не писалось и не рассматривалось

diletant10 в сообщении #523060 писал(а):

С Земли запустили космический аппарат - матку (КА-М). На круговую орбиту вокруг Солнца на расстоянии от Солнца в разы большем, чем максимальное удаление Плутона от Солнца. Плоскость орбиты КА-Ми совпадает с плоскостью орбиты Юпитера. На КА-Ме две одинаковые ракеты.

diletant10 в сообщении #524018 писал(а):

Я в недоумении. Разве в СТО какая-либо ИСО имеет преимущество? Насколько я понимаю в СТО, неподвижным наблюдателем можно считать не только космический аппарат – матку, но и любую из двух ракет. Вы меня запутали.

Что-то Вас подозрительно легко запутать. У меня и в мыслях не было этого. Разумеется, в СТО (как и в классической механике) все ИСО равноправны.

diletant10 в сообщении #524018 писал(а):

Хорошо, принято. Заменим формулировку. Часы на обеих ракетах идут с одинаковой скоростью?

Часы одинаковые. Вопрос о том, одинаково ли они идут, требует определённых уточнений: в каком смысле - одинаково. Можно придумать процедуру сравнения, которая покажет, что одинаково (придумайте сами; в моих сообщениях в этой теме можете найти подсказку).

diletant10 в сообщении #524018 писал(а):

То бишь, о чем я писал в сообщении от 04.01.2012, 22:17. Но в таком случае, где же замедление времени в первой ракете относительно хода времени в ИСО второй ракеты, в которой вторая ракета неподвижна, а первая ракета удаляется от нее с постоянной скоростью?

Посмотрите моё сообщение http://dxdy.ru/post523355.html#p523355. И не только посмотрите, но и внимательно почитайте.
Я начну с внесения поправки в то сообщение. Я несколько поторопился утверждением (Вы его найдёте в конце того сообщения)

Someone в сообщении #523355 писал(а):

(и будет видеть правую ракету на расстоянии $t_0v_2=\frac{120}{41}$ светового года).

В действительности это расстояние, на котором правая ракета находится от левой в данный момент по часам левой ракеты, но сигнал оттуда ещё не дошёл. С какого расстояния он дошёл, можно найти так. Обозначим $v$ скорость удаления правой ракеты от левой, $d$ - расстояние, с которого пришёл сигнал (это то расстояние, на котором пассажир левой ракеты видит правую), $t$ - момент наблюдения (все величины измеряются в ИСО левой ракеты). Правой ракете потребовалось время $\frac dv$, чтобы добраться до точки, где её увидели, и сигналу потребовалось время $\frac dc$, чтобы добраться оттуда до левой ракеты. Получаем уравнение $\frac dv+\frac dc=t$, откуда $d=\frac{vt}{1+\frac vc}$. Подставляя $v=v_2=\frac{40}{41}c$ и $t=t_0=3$ года, получим $d=\frac{\frac{40}{41}c\cdot 3}{1+\frac{40}{41}}=\frac{40}{27}c$.

Итак, находясь в точке поворота спустя $t_0=3$ года после старта, наблюдатель в левой ракете видит правую на расстоянии $\frac{40}{27}$ светового года, а подсчитав полученные от неё сигналы, знает, что там прошло $\frac 19t_0=\frac 13$ года. $\frac{40}{27}$ года потребовалось сигналу, чтобы дойти от правой ракеты до левой, поэтому отправлен он был тогда, когда часы в левой ракете показывали $3-\frac{40}{27}=\frac{41}{27}$ года. Поскольку часы в правой ракете в момент отправления сигнала показывали $\frac 13$ года (в $\frac{41}{27}{:}\frac 13=\frac{41}{9}$ раза меньше), то мы и наблюдаем искомое замедление времени. Коэффициент замедления при скорости $v_2=\frac{40}{41}c$ равен $\sqrt{1-\frac{v_2^2}{c^2}}=\sqrt{1-\frac{40^2}{41^2}}=\frac 9{41}$, что согласуется с полученным нами результатом.

diletant10 в сообщении #524018 писал(а):

Не понял. Разве СО, в которой свободно падающее тело в гравитационном поле планеты неподвижно, является ИСО?

Видите ли, точных ИСО вообще не бывает. Вопрос лишь в том, насколько близка используемая СО к инерциальной. В большинстве случаев систему отсчёта, связанную с вращающейся Землёй, можно с достаточной точностью считать инерциальной, хотя при желании можно продемонстрировать её неинерциальность с помощью маятника Фуко (наличие силы тяжести инерциальность практически не нарушает, так как гравитационные эффекты очень малы). В том эксперименте, о котором я писал, вращение Земли и гравитация вообще никакой роли не играют. Можете подсчитать сами, на сколько отклонится траектория частиц за время пролёта семисот метров из-за влияния силы тяжести или поворота Земли.

[diletant10]

(Оффтоп)

Someone в сообщении #524049 писал(а):

Что-то Вас подозрительно легко запутать. У меня и в мыслях не было этого.

В своей профессии я профессионал. К моему мнению прислушиваются и с моим мнением считаются. Зачастую мое мнение бывает решающим. И это нормально. И сам привык прислушиваться к мнению других профессионалов, коим я считаю Вас, коль скоро Вы Заслуженный участник Форума. В СТО я далеко не профессионал. Поэтому есть вопросы. Что касается ОТО, там даже не любитель. Поэтому и вопросов нет. Смогу начать ОТО осваивать, появятся вопросы и по ОТО. Поверьте на слово, зря подозреваете!!!

[diletant10]

Someone в сообщении #524049 писал(а):

В том эксперименте, о котором я писал, вращение Земли и гравитация вообще никакой роли не играют.

Выделено мною. У меня другое мнение насчет роли гравитации. Смотрите
http://ufn.ru/ru/articles/1989/7/f/
в частности, формулы (6.3) и (8.1).
При приближении скорости частицы весьма близко к световой сила гравитационного взаимодействия частицы и Земли растет настолько катастрофически, что считать СО, в которой частица неподвижна, инерциальной? А как же Ваше

Someone в сообщении #523920 писал(а):

diletant10 в сообщении #523754 писал(а):

Вопрос. СО второй ракеты, где вторая ракета неподвижна, является ИСО?

Если её двигатели не работают и никакие внешние силы на неё не действуют, то является.

Выделено мною. А в приведенном Вами эксперименте, с пионом, силы, действующие на частицы (массовые) настолько велики, что, извините, по моему скромному мнению, не допускают использование СТО. Даже для оценки…. Там нет ИСО. Даже в грубом приближении.

Someone в сообщении #524049 писал(а):

Разумеется, в СТО (как и в классической механике) все ИСО равноправны.

Коль скоро так, то…. Одинаковые часы во всех ИСО идут с одинаковой скоростью, то есть, скорость процессов при одинаковых условиях во всех ИСО одна и та же!!! Поясню ход рассуждений. Есть некоторое количество одинаковых часов в одной и той же ИСО. И неподвижных в данной ИСО. Соответственно, неподвижны относительно друг друга. И была проведена процедура их синхронизации. На всех часах одинаковая дата и одинаковое время. И ход часов одинаков.

Someone в сообщении #523920 писал(а):

Процедура синхронизации работоспособна только для часов, которые неподвижны относительно друг друга (и движутся на неизменном расстоянии по инерции).

Затем все часы привели в движение относительно первоначальной ИСО в различных направлениях и с различными, но постоянными скоростями относительно как первоначальной ИСО, так и относительно друг друга. То есть, для каждых часов есть собственная ИСО, в которой они неподвижны. А остальные часы в этой же ИСО движутся равномерно. С разными, но неменяющимися скоростями, и в различных, но неменяющихся направлениях. Иначе, СО каждых часов есть ИСО. Но

Someone в сообщении #523920 писал(а):

Движущиеся относительно друг друга часы не могут быть синхронизированы.

Поэтому, на различных часах может быть различная дата и время. Однако, скорость хода часов во всех наших ИСО остается одной и той же. Равной скорости их хода да их разлета от первоначальной ИСО, где проводилась синхронизация их, которой не стало после их разлета. Из-за разных условий разлета. Но, извините, повторюсь,

Someone в сообщении #524049 писал(а):

Разумеется, в СТО (как и в классической механике) все ИСО равноправны.

Иначе, хоть показания часов могут быть разными, но скорость их хода одинаковая. Отсюда, по моему скромному мнению, следует вывод, что реального замедления времени в первой ракете относительно времени во второй ракете нет. Все ИСО равноправны. То есть, в СТО есть лишь наблюдаемое замедление времени из-за конечности скорости света. Реального же замедления нет. В противном случае, запустив некое множество часов в «свободное плавание» в космосе, можно пытаться выделить АСО, что противно СТО. И не только.

Цитата:

Посмотрите моё сообщение http://dxdy.ru/post523355.html#p523355. И не только посмотрите, но и внимательно почитайте.

Посмотрел, почитал. Вопросов нет. В приводимые Вами расчетах меняется как модуль скорости, так и вектор. И это, по моему скромному мнению, не только СТО.

Цитата:

Видите ли, точных ИСО вообще не бывает. Вопрос лишь в том, насколько близка используемая СО к инерциальной.

И предваряя такое замечание, я так акцентировал внимание на процессе запуска двух ракет. Смотрим первую и вторую ситуацию в моем сообщении
http://dxdy.ru/post523060.html#p523060
И чтобы условия в обеих ракетах были одинаковы. Разные у них лишь векторы скоростей относительно друг друга.