Предположим, данная последовательность к чему-то сходится относительно равномерной нормы. Тогда она непременно сходится к элементу данного пространства в силу его полноты относительно равномерной нормы. То есть она сходится к непрерывной функции. Но выше было установлено, что она сходится к разрывной функции - противоречие.
Ничего не понятно: сходимость по
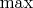
-норме означает равномерную сходимость. В
![$C([-1;1])$ $C([-1;1])$](https://dxdy-02.korotkov.co.uk/f/5/b/d/5bd549f3dfa36f25799d7032cf2ae8da82.png)
с указанной нормой упомянутая выше последовательность не сходится.
Когда мы говорим о какой-либо сходимости (равномерной и т.д.)
Смотря как Вы определяете сходимость. Насколько я помню, дело обстоит следующим образом: определить
сходимость последовательности в ЛП означает задать в нем структуру
равномерного пространства. Но не любое равномерное пространство нормируемо.
Навскидку: поточечная сходимость задает ненормируемую равномерность на
![$C([-1;1])$ $C([-1;1])$](https://dxdy-02.korotkov.co.uk/f/5/b/d/5bd549f3dfa36f25799d7032cf2ae8da82.png)



