Всюду, всюду, не сомневайтесь. Мне даже кажется, что я когда-то давно-давно здесь на форуме построение излагал. Но как теперь это найти - не представляю.
незванный гость писал(а):
:evil:
А можно, раз уж пошла такая пьянка, пример функции, дифференцируемой всюду на отрезке, и производная которой не непрерывна?
Пусть

- последовательность, взаимно однозначно перечисляющая все рациональные числа. Обозначим
![$M_n=\max\{|\sqrt[3]{x-r_n}|:-n\leqslant x\leqslant n\}$ $M_n=\max\{|\sqrt[3]{x-r_n}|:-n\leqslant x\leqslant n\}$](https://dxdy-01.korotkov.co.uk/f/8/f/0/8f044afd06df47e92aee36eb6e5b33a982.png)
. Функция
![$$f(x)=\sum\limits_{n\in\mathbb N}\frac{\sqrt[3]{x-r_n}}{n^2M_n}$$ $$f(x)=\sum\limits_{n\in\mathbb N}\frac{\sqrt[3]{x-r_n}}{n^2M_n}$$](https://dxdy-02.korotkov.co.uk/f/9/8/d/98d7cb4d38b5f74fdb916428a3772d1e82.png)
на всей числовой оси

непрерывна, так как ряд в правой части равномерно сходится на каждом отрезке
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
, и (строго) возрастает; множество значений функции

совпадает с

. Из всего этого следует, что существует обратная функция

, которая также непрерывна и возрастает на всей числовой оси

.
Для функции

во всех точках существует предел

(может быть,

, например, как в рациональных точках), поэтому, по теореме о производной обратной функции, обобщённой для случая таких бесконечных производных, обратная функция имеет всюду конечную производную

.
Легко видеть, что
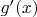
на всюду плотном множестве

равна

, и в то же время не может быть равна

во всех точках какого-нибудь интервала

, так как

возрастает на всём

. Поэтому
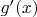
не может быть непрерывной ни на каком интервале.
Можно привести и совсем простой пример:

Тогда
